【题目】(2016山西省第23题)综合与探究
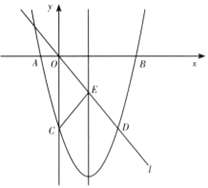
如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使![]() ≌
≌![]() ,若存在,请直接写出点F的坐标;若不存在,请说明理由;
,若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q.试探究:当m为何值时,![]() 是等腰三角形.
是等腰三角形.
参考答案:
【答案】(1)、![]() ;B(8,0);E(3,-4);(2)、(
;B(8,0);E(3,-4);(2)、(![]() )或(
)或(![]() );(3)、
);(3)、![]() 或
或![]() .
.
【解析】
试题分析:(1)、将A,D的坐标代入函数解析式,解二元一次方程即可求出函数表达式;点B坐标:利用抛物线对称性,求出对称轴结合A点坐标即可求出B点坐标;点E坐标:E为直线l和抛物线对称轴的交点,利用D点坐标求出l表达式,令其横坐标为![]() ,即可求出点E的坐标;(2)、利用全等对应边相等,可知FO=FC,所以点F肯定在OC的垂直平分线上,所以点F的纵坐标为-4,带入抛物线表达式,即可求出横坐标;(3)、根据点P在y轴负半轴上运动,∴分两种情况讨论,再结合相似求解.
,即可求出点E的坐标;(2)、利用全等对应边相等,可知FO=FC,所以点F肯定在OC的垂直平分线上,所以点F的纵坐标为-4,带入抛物线表达式,即可求出横坐标;(3)、根据点P在y轴负半轴上运动,∴分两种情况讨论,再结合相似求解.
试题解析:(1)![]() 抛物线
抛物线![]() 经过点A(-2,0),D(6,-8),
经过点A(-2,0),D(6,-8),
![]() 解得
解得![]()
![]() 抛物线的函数表达式为
抛物线的函数表达式为![]()
![]()
![]() ,
,![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() .又
.又![]() 抛物线与x轴交于A,B两点,点A的坐标为(-2,0).
抛物线与x轴交于A,B两点,点A的坐标为(-2,0).![]() 点B的坐标为(8,0)
点B的坐标为(8,0)
设直线l的函数表达式为![]() .
.![]() 点D(6,-8)在直线l上,
点D(6,-8)在直线l上,![]() 6k=-8,解得
6k=-8,解得![]() .
.
![]() 直线l的函数表达式为
直线l的函数表达式为![]()
![]() 点E为直线l和抛物线对称轴的交点.
点E为直线l和抛物线对称轴的交点.![]() 点E的横坐标为3,纵坐标为
点E的横坐标为3,纵坐标为![]() ,
,
即点E的坐标为(3,-4)
(2)、抛物线上存在点F,使![]() ≌
≌![]() .点F的坐标为(
.点F的坐标为(![]() )或(
)或(![]() )
)
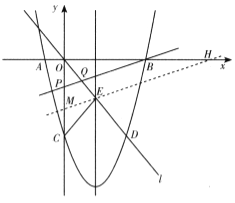
(3)、分两种情况:
①当![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
![]() 点E的坐标为(3,-4),
点E的坐标为(3,-4),![]() ,过点E作直线ME//PB,交y轴于点M,交x轴于点H,则
,过点E作直线ME//PB,交y轴于点M,交x轴于点H,则![]() ,
,![]()
![]() 点M的坐标为(0,-5).
点M的坐标为(0,-5).
设直线ME的表达式为![]() ,
,![]()
![]() ,解得
,解得![]() ,
,![]() ME的函数表达式为
ME的函数表达式为![]() ,令y=0,得
,令y=0,得![]() ,解得x=15,
,解得x=15,![]() 点H的坐标为(15,0)
点H的坐标为(15,0)
又![]() MH//PB,
MH//PB,![]()
![]() ,即
,即![]() ,
,![]()
![]()
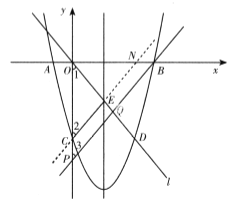
②当![]() 时,
时,![]() 是等腰三角形. 当x=0时,
是等腰三角形. 当x=0时,![]() ,
,![]() 点C的坐标为(0,-8),
点C的坐标为(0,-8),
![]()
![]() ,
,![]() OE=CE,
OE=CE,![]()
![]() ,又因为
,又因为![]() ,
,![]()
![]() ,
, ![]()
![]() ,
,![]() CE//PB
CE//PB
设直线CE交x轴于点N,其函数表达式为![]() ,
,![]()
![]() ,解得
,解得![]() ,
,
![]() CE的函数表达式为
CE的函数表达式为![]() ,令y=0,得
,令y=0,得![]() ,
,![]()
![]() ,
,![]() 点N的坐标为(6,0)
点N的坐标为(6,0)
![]() CN//PB,
CN//PB,![]()
![]() ,
,![]()
![]() ,解得
,解得![]()
综上所述,当m的值为![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数2,3,x,5,6五个数的平均数为4,则x的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某经济开发区今年1月份工业产值达50亿元,第一季度总产值175亿元,问二三月份月平均增长率是多少?设平均每月增长的百分率为x,根据题意得方程_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图3,直线AB、CD相交于点O,∠AOE=90°,从给出的A、B、C三个答案中选择适当答案填空.

(1)∠1与∠2的关系是( )
(2)∠3与∠4的关系是( )
(3)∠3与∠2的关系是( )
(4)∠2与∠4的关系是( )
A.互为补角 B.互为余角 C.即不互补又不互余
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016贵州省毕节市第25题)阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.

问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线
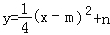 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式2x3-8x2+x-1与多项式3x3+2mx2-5x+3的和不含二次项,则m为( )
A. 2 B. -2 C. 4 D. -4
-
科目: 来源: 题型:
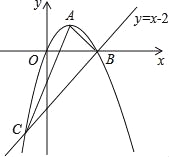
查看答案和解析>>【题目】(2016广西省南宁市第24题)如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
相关试题

