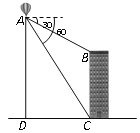
【题目】热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为420米,求这栋楼的高度.
参考答案:
【答案】280.
【解析】试题分析:过A作AE⊥BC,交CB的延长线于点E,在Rt△ACD中,求出CD的长,则AE=CD,在Rt△ABE中,求出BE的长,然后根据BC=AD﹣BE即可得到这栋楼的高度.
试题解析:过A作AE⊥BC,交CB的延长线于点E,在Rt△ACD中,∵∠CAD=30°,AD=420米,∴CD=ADtan30°=![]() =
=![]() (米),∴AE=CD=
(米),∴AE=CD=![]() 140
140![]() 米.在Rt△ABE中,∵∠BAE=30°,AE=
米.在Rt△ABE中,∵∠BAE=30°,AE=![]() 米,∴BE=AEtan30°=
米,∴BE=AEtan30°=![]() ×
×![]() =140(米),∴BC=AD﹣BE=420﹣140=280(米).
=140(米),∴BC=AD﹣BE=420﹣140=280(米).
答:这栋楼的高度为280米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
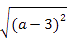 =8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少?
=8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°,
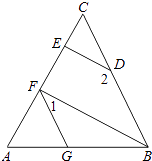
(1)求证;BF∥DE.
(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数据中,四个数成比例的是( )
A. 3,2,4,9B. 1,2,3,6C. 1,2,3,4D. 5,8,2,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式xm﹣1y3与4xyn的和是单项式,则mn的值是( )
A.3
B.6
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程2x-1=3x+2的解为 ( )
A. x=1 B. x=-1 C. x=-3 D. x=3
相关试题

