【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )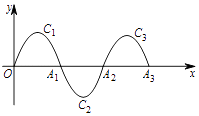
A.﹣1
B.0
C.1
D.不确定
参考答案:
【答案】C
【解析】解:∵一段抛物线C1:y=﹣x(x﹣2)(0≤x≤2),
∴图象C1与x轴交点坐标为:(0,0),(2,0),
∵将C1绕点A1旋转180°得C2,交x轴于点A2;,
∴抛物线C2:y=(x﹣2)(x﹣4)(2≤x≤4),
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
∴P(2017,m)在抛物线C1009上,
∵n=1009是奇数,
∴P(2017,m)在x轴的上方,m=1,
∴当x=2017时,m=1.
所以答案是:C,
【考点精析】根据题目的已知条件,利用二次函数图象的平移和抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
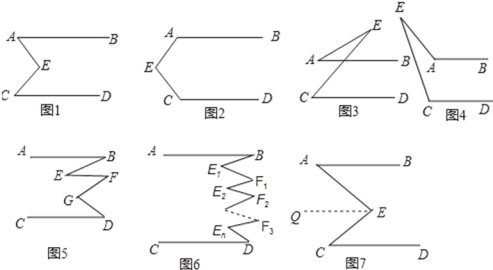
查看答案和解析>>【题目】小红和小明在研究一个数学问题:已知AB∥CD,AB和CD都不经过点E,探索∠E与∠A,∠C的数量关系.
(一)发现:在如图1中,小红和小明都发现:∠AEC=∠A+∠C;
小红是这样证明的:如图7过点E作EQ∥AB.
∴∠AEQ=∠A( )
∵EQ∥AB,AB∥CD.
∴EQ∥CD( )
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C.
小明是这样证明的:如图7过点E作EQ∥AB∥CD.
∴∠AEQ=∠A,∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
请在上面证明过程的横线上,填写依据:两人的证明过程中,完全正确的是 .
(二)尝试:
(1)在如图2中,若∠A=110°,∠C=130°,则∠E的度数为 ;
(2)在如图3中,若∠A=20°,∠C=50°,则∠E的度数为 .
(三)探索:
装置如图4中,探索∠E与∠A,∠C的数量关系,并说明理由.
(四)猜想:
(1)如图5,∠B、∠D、∠E、∠F、∠G之间有什么关系?(直接写出结论)
(2)如图6,你可以得到什么结论?(直接写出结论)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:
我们知道,
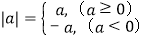 于是要解不等式
于是要解不等式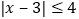 ,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:解:(1)当
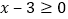 ,即
,即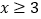 时:
时: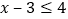
解这个不等式,得:
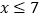
由条件
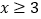 ,有:
,有:
(2)当
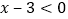 ,即
,即 时,
时,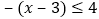
解这个不等式,得:
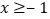
由条件
 ,有:
,有: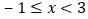
∴ 如图,

综合(1)、(2)原不等式的解为:
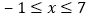
根据以上思想,请探究完成下列
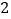 个小题:
个小题: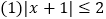 ;
;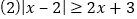
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=7,EF=3,则BC长为( )
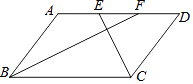
A.9
B.10
C.11
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点
 表示的数为
表示的数为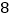 ,
,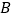 是数轴上位于点
是数轴上位于点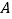 左侧一点,且AB=20,动点
左侧一点,且AB=20,动点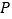 从
从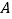 点出发,以每秒
点出发,以每秒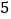 个单位长度的速度沿数轴向左匀速运动,设运动时间t(t>0)秒.
个单位长度的速度沿数轴向左匀速运动,设运动时间t(t>0)秒.
(1)写出数轴上点
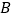 表示的数______;点
表示的数______;点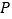 表示的数_______(用含
表示的数_______(用含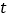 的代数式表示)
的代数式表示)(2)动点
 从点
从点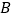 出发,以每秒
出发,以每秒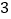 个单位长度的速度沿数轴向右匀速运动,若点
个单位长度的速度沿数轴向右匀速运动,若点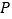 、
、 同时出发,问多少秒时
同时出发,问多少秒时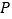 、
、 之间的距离恰好等于
之间的距离恰好等于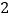 ?
?(3)动点
 从点
从点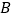 出发,以每秒
出发,以每秒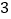 个单位长度的速度沿数轴向左匀速运动,若点
个单位长度的速度沿数轴向左匀速运动,若点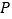 、
、 同时出发,问多少秒时
同时出发,问多少秒时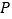 、
、 span>之间的距离恰好又等于
span>之间的距离恰好又等于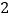 ?
?(4)若
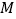 为
为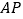 的中点,
的中点, 为
为 的中点,在点
的中点,在点 运动的过程中,线段
运动的过程中,线段 的长度是否发生变化?若变化,请说明理由,若不变,请画出图形,并求出线段
的长度是否发生变化?若变化,请说明理由,若不变,请画出图形,并求出线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
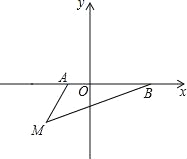
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=
 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,A(1,3),B(2,1),直角坐标系中存在点C,使得O,A,B,C四点构成平行四边形,则C点的坐标为______________________________.

相关试题

