搜索
【题目】如图，2条直线 最多有
＝1个交点，3条直线最多有
＝3个交点，4条直线最多有
＝6个交点，……由此猜想，8条直线最多有＿＿＿个交点.
A. 32 B. 16 C. 28 D. 40
参考答案：
【答案】C
【解析】
由已知中两条相交直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点点，五条直线最多有10个交点，我们分析n值变化过程中，交点最多个数的变化趋势，找出规律后，归纳为一般性公式即可得到答案．
令n条直线最多交点个数为M：
两条相交直线最多有1个交点，即n=2，M=1，
三条直线最多有3个交点，即n=3，M=3，
四条直线最多有6个交点点，即n=4，M=6，
五条直线最多有10个交点，即n=5，M=10，
…
则n条直线最多交点个数M=1+2+3+4+…+（n-1）=
，
当n=8时，
=28，
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB∥CD.
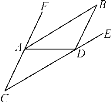
(1)判断∠FAB与∠C的大小关系，请说明理由；
(2)若∠C＝35°，AB是∠FAD的平分线．
①求∠FAD的度数；
②若∠ADB＝110°，求∠BDE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A、B两点的坐标分别为（2，0）、（0，4），P是△AOB外接圆⊙C上的一点，且∠AOP=45°，则点P的坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克，大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元，小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后，该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克，进价不变，但在运输过程中小樱桃损耗了20%．若小樱桃的售价不变，要想让第二次赚的钱不少于第一次所赚钱的90%，大樱桃的售价最少应为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（7分）如图所示，O是直线AB上一点，∠AOC=
∠BOC，OC是∠AOD的平分线．
（1）求∠COD的度数．
（2）判断OD与AB的位置关系，并说出理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校学生在电脑培训前后各参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，随机抽取其中32名学生两次考试考分等级制成统计图（如图），试回答下列问题：
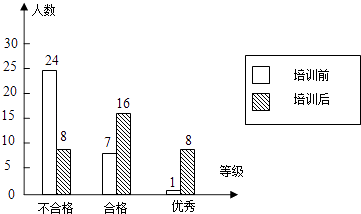
（1）这32名学生经过培训，考分等级“不合格”的百分比由下降到；
（2）估计该校640名学生，培训后考分等级为“合格”与“优秀”的学生共有多少名． -
科目： 来源： 题型：
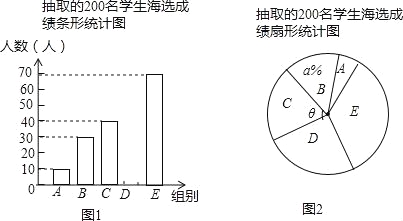
查看答案和解析>>【题目】中华文明，源远流长；中华诗词，寓意深广．为了传承优秀传统文化，我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次海选比赛的成绩分布情况，随机抽取了其中200名学生的海选比赛成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列统计图表：
抽取的200名学生海选成绩分组表
组别
海选成绩x
A组
50≤x＜60
B组
60≤x＜70
C组
70≤x＜80
D组
80≤x＜90
E组
90≤x＜100
请根据所给信息，解答下列问题：
（1）请把图1中的条形统计图补充完整；（温馨提示：请画在答题卷相对应的图上）
（2）在图2的扇形统计图中，记表示B组人数所占的百分比为a%，则a的值为 ，表示C组扇形的圆心角θ的度数为 度；
（3）规定海选成绩在90分以上（包括90分）记为“优等”，请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人？
相关试题
