【题目】已知:![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() ,请回答问题:
,请回答问题:
(1)请直接写出![]() 、
、![]() 、
、![]() 的值.
的值.![]() ,
,![]() ,
,![]() .
.
(2)![]() 、
、![]() 、
、![]() 所对应的点分别为
所对应的点分别为![]() 、
、![]() 、
、![]() ,点
,点![]() 为一动点,其对应的数为
为一动点,其对应的数为![]() ,点
,点![]() 在
在![]() 、
、![]() 之间运动时,请化简式子:
之间运动时,请化简式子:![]() (请写出化简过程)
(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,假设经过
个单位长度的速度向右运动,假设经过![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .请问:
.请问:![]() 的值是否随着时间的变化而改变?若变化,请说明理由:若不变,请求其值.
的值是否随着时间的变化而改变?若变化,请说明理由:若不变,请求其值.
参考答案:
【答案】(1)-1,1,6;(2)-10;(3)不变,值为3.
【解析】
(1)根据最小的正整数是1,推出b=1,再利用非负数的性质求出a、c即可.
(2)首先确定x的范围,再化简绝对值即可.
(3)BCAB的值不变.根据题意用n,t表示出BC、AB即可解决问题.
解:∵b是最小的正整数,
∴b=1,
∵(c6)2+|a+b|=0,(c6)20,|a+b|0,
∴c=6,a=1,b=1,
故答案为1,1,6;
(2).由题意1<x<1,
∴|x+1||x1|2|x+5|=x+1+x12x10=10.
(3)不变,
由题意BC=5+5nt2nt=5+3nt,AB=nt+2+2nt=2+3nt,
∴BCAB=(5+3nt)(2+3nt)=3,
∴BCAB的值不变,BCAB=3.
-
科目: 来源: 题型:
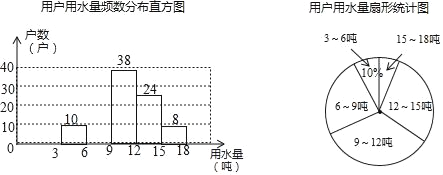
查看答案和解析>>【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 ;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.

(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.
(1)体育场离小强家有多远?小强从家到体育场用了多长时间?
(2)体育场距文具店多远?
(3)小强在文具店逗留了多长时间?
(4)小强从文具店回家的平均速度是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )

A、小莹的速度随时间的增大而增大B、小梅的平均速度比小莹的平均速度大
C、在起跑后180秒时,两人相遇D、在起跑后50秒时,小梅在小莹的前面
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN于点E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.

相关试题

