Question

【题目】如图，点E在直线DF上，点B在直线AC上，若∠AGB=∠EHF，∠C=∠D．

则∠A=∠F，请说明理由．

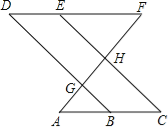
解：∵∠AGB=∠EHF

∠AGB= （对顶角相等）

∴∠EHF=∠DGF

∴DB∥EC

∴∠ =∠DBA （ 两直线平行，同位角相等）

又∵∠C=∠D

∴∠DBA=∠D

∴DF∥ （内错角相等，两直线平行）

∴∠A=∠F ．

Answer 1

【答案】已知；∠DGF；同位角相等，两直线平行；C；AC；两直线平行，内错角相等

【解析】试题分析：根据对顶角相等推出同位角∠EHF=∠DGF，从而证得两直线DB∥EC；然后由平行线的性质知内错角∠DBA=∠D，即可根据平行线的判定定理得两直线DF∥AC，最后由平行线的性质证得：∠A=∠F.

试题解析：∵∠AGB=∠EHF（已知），∠AGB=∠DGF（对顶角相等），

∴∠EHF=∠DGF

∴DB∥EC（同位角相等，两直线平行），

∴∠C="∠DBA" （ 两直线平行，同位角相等）；

又∵∠C=∠D（已知），

∴∠DBA=∠D（等量代换），

∴DF∥AC（内错角相等，两直线平行），

∴∠A=∠F（两直线平行，内错角相等）；