搜索
【题目】如图，在平面直角坐标系中，直线y=kx+b与x轴交于点A，与y轴交于点B，且四边形AOBC是矩形，BC=6，矩形AOBC的面积为18．
（1）求线段OC的长．
（2）求直线AB的解析式．
参考答案：
【答案】（1）3
；（2）y=﹣
x+3．
【解析】
试题分析：（1）先根据矩形的性质和矩形的面积公式可求OB=3，在Rt△OBC中，根据勾股定理得线段OC的长．
（2）根据待定系数法可求直线AB的解析式．
解：（1）∵矩形AOBC的面积为18，BC=6，
∴∠OBC=90°，OBBC=18，
∴OB=3．
在Rt△OBC中，根据勾股定理得
OC=
=
=3；
（2）∵四边形AOBC是矩形，
∴BC=OA=6，
∴A（6，0），B（0，3），
∵直线y=kx+b与x轴交于点A，与y轴交于点B，
∴
，
解得
．
∴直线AB的解析式为y=﹣x+3．
-
科目： 来源： 题型：
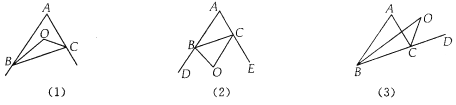
查看答案和解析>>【题目】 在△ABC中，∠A＝40°．
（1）如图(1)BO、CO是△ABC的内角角平分线，且相交于点O，求∠BOC；
（2）如图(2)若BO、CO是△ABC的外角角平分线，且相交于点O，求∠BOC；
（3）如图(3)若BO、CO分别是△ABC的一内角和一外角角平分线，且相交于点O，求∠BOC；
（4）根据上述三问的结果，当∠A＝n°时，分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题8分）如下图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．
（1）△ABC的面积为 ；
（2）将△ABC经过平移后得到△A′B′C′，图中标出了点B的对应点B'，补全△A′B′C′；
（3）在图中画出△ABC的高CD；
（4）若连接
， 
，则这两条线段之间的关系是 ； （5）能使S△ABC＝S△QBC的格点Q，共有 个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的角平分线 CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②CA平分∠BCG；③∠ADC＝∠GCD；④∠DFB＝
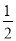∠CGE．其中正确的结论是( )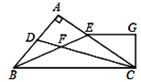
A. ①③ B. ②④ C. ①③④ D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】点M(2，3)关于y轴对称的点的坐标为（ ）
A. (- 2，- 3) B. (2，- 3) C. (- 2，3) D. (3，- 2)
-
科目： 来源： 题型：
查看答案和解析>>【题目】 （2016黑龙江哈尔滨第14题）把多项式ax2+2a2x+a3分解因式的结果是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】目前发现一种病毒直径约是0.0000252米，将0.0000252用科学记数法表示为 ．
相关试题
