搜索
【题目】（本题8分）如下图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．
（1）△ABC的面积为 ；
（2）将△ABC经过平移后得到△A′B′C′，图中标出了点B的对应点B'，补全△A′B′C′；
（3）在图中画出△ABC的高CD；
（4）若连接
， 
，则这两条线段之间的关系是 ；
（5）能使S△ABC＝S△QBC的格点Q，共有 个．
参考答案：
【答案】（1）8 ；（2）、答案见解析；（3）、平行且相等；（4）、答案见解析；（5）、4
【解析】试题分析：（1）、根据三角形的面积求法求出面积；（2）、根据平移的法则画出图形；（3）、根据平移的性质得出线段的关系；（4）、根据三角形高线的画法画出图形；（5）、根据面积相等的法则求出点Q的个数.
试题解析：（1）、S=4×4÷2=8
（2）、答案见图形；
（3）、平行且相等
（4）、答案见图形
（5）、4
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题满分8分）已知：如图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系： ；
（2）仔细观察，在图2中“8字形”的个数： 个；
（3）在图2中，若∠D=40°，∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．利用（1）的结论，可求得∠P的度数是 ；
（4）如果图2中∠D和∠B为任意角时，其他条件不变，请直接写出∠P与∠D、∠B之间存在的数量关系是 ．
-
科目： 来源： 题型：
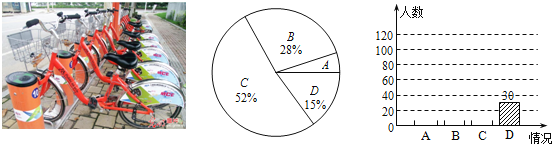
查看答案和解析>>【题目】“低碳环保，你我同行”，两年来，南京市区的公共自行车给市民出行带来切实方便，电视台记者在某区街头随机选取了市民进行调查，调查的问题是“您大概多九使用一次公共自行车？”，将本次调查结果归为四种情况：A．每天都用；B．经常使用；C．偶尔使用；D．从未使用．将这次调查情况整理并绘制如下两幅统计图：
根据图中的信息，解答下列问题：
（1）本次活动共有 位市民参与调查；
（2）补全条形统计图；
（3）根据统计结果，若该区有46万市民，请估算每天都用公共自行车的市民约有多少人？
考点：条形统计图；用样本估计总体；扇形统计图．
-
科目： 来源： 题型：
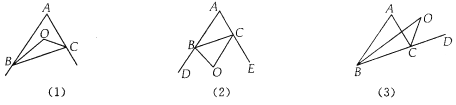
查看答案和解析>>【题目】 在△ABC中，∠A＝40°．
（1）如图(1)BO、CO是△ABC的内角角平分线，且相交于点O，求∠BOC；
（2）如图(2)若BO、CO是△ABC的外角角平分线，且相交于点O，求∠BOC；
（3）如图(3)若BO、CO分别是△ABC的一内角和一外角角平分线，且相交于点O，求∠BOC；
（4）根据上述三问的结果，当∠A＝n°时，分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的角平分线 CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②CA平分∠BCG；③∠ADC＝∠GCD；④∠DFB＝
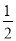∠CGE．其中正确的结论是( )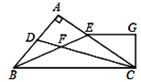
A. ①③ B. ②④ C. ①③④ D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线y=kx+b与x轴交于点A，与y轴交于点B，且四边形AOBC是矩形，BC=6，矩形AOBC的面积为18．
（1）求线段OC的长．
（2）求直线AB的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点M(2，3)关于y轴对称的点的坐标为（ ）
A. (- 2，- 3) B. (2，- 3) C. (- 2，3) D. (3，- 2)
相关试题
