【题目】如图,在半径为 ![]() 的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )
的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( ) 
A.1
B.![]()
C.2
D.2 ![]()
参考答案:
【答案】B
【解析】解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图, 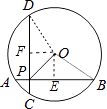
则AE=BE= ![]() AB=2,DF=CF=
AB=2,DF=CF= ![]() CD=2,
CD=2,
在Rt△OBE中,∵OB= ![]() ,BE=2,
,BE=2,
∴OE= ![]() =1,
=1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
而OE=OF=1,
∴四边形OEPF为正方形,
∴OP= ![]() OE=
OE= ![]() .
.
故选B.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
-
科目: 来源: 题型:
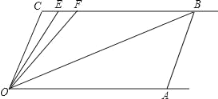
查看答案和解析>>【题目】如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
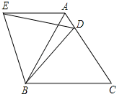
A.②③④B.①②④C.①②③D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
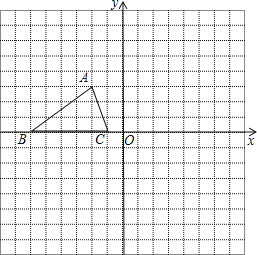
(1)请直接写出点A关于y轴对称的点的坐标为 ;
(2)将△ABC平移,使点B移动后的坐标为B′(﹣5,﹣5),画出平移后的图形△A′B′C′;
(3)将△ABC绕坐标原点O顺时针旋转90°,画出旋转后的图形△A″B″C″.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(-1,0),B(-3,-3),若BC∥OA,且BC=4OA.
(1)求点C的坐标;
(2)求△ABC的面积.
相关试题

