【题目】如图,△ABC中,∠ABC和∠ACB的角平分线相交于点O,DE经过O点,且DE//BC.
⑴请指出图中的两个等腰三角形.
⑵请选择⑴中的一个三角形,说明它是等腰三角形的理由.
⑶如果△ABC的周长是26,△ADE的周长是18,请求出BC的长.

参考答案:
【答案】(1)△BOD和△COE;(2)证明见解析;(3)8.
【解析】试题分析:(1)△BOD和△COE是等腰三角形
(2)根据角平分线和平行线的性质来证明;
(3)由(2)的结论代入到△ABC的周长中,列方程,可以得出BC的长.
解:(1)△BOD和△COE;
(2)∵BO是∠ABC的平分线,
∴∠DBO=∠OBC,
又∵DE//BC,
∴∠DOB=∠OBC,
∴∠DBO=∠DOB,
∴BD=OD,
∴△BOD 是等腰三角形;
同理可得:△COE是等腰三角形;
(3)∵△BOD和△COE是等腰三角形,
∴BD=OD,CE=OE,
∴BD+CE=OD+OE,
即 BD+CE=DE,
∵△ABC的周长=AD+BD+BC+AE+CE=AD+BC+AE+DE=△ADE的周长+BC,
又∵△ABC的周长是26,△ADE的周长是18,
∴26=18+BC,
∴BC=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于
 CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )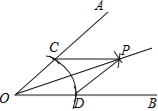
A. SAS B. ASA C. AAS D. SSS
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种数字化的信息传输中,先将信息转化为由数字
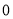 和
和 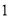 组成的数字串,并对数字串进行加密后再传输.现采用一种简单的加密方法:将原有的每个
组成的数字串,并对数字串进行加密后再传输.现采用一种简单的加密方法:将原有的每个  都变成
都变成  ,原有的每个
,原有的每个 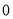 都变成
都变成  .我们用
.我们用  表示没有经过加密的数字串.这样对
表示没有经过加密的数字串.这样对 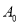 进行一次加密就得到一个新的数字串
进行一次加密就得到一个新的数字串  ,对
,对  再进行一次加密又得到一个新的数字串
再进行一次加密又得到一个新的数字串 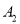 ,依此类推,
,依此类推, 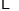 .例如
.例如 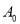 :
: 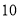 ,则
,则 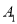 :
: 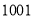 .若已知
.若已知 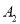 :
: 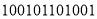 ,则
,则  ________________;若数字串
________________;若数字串  共有
共有  个数字,则数字串
个数字,则数字串  中相邻两个数字相等的数对至少有________________对.
中相邻两个数字相等的数对至少有________________对. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段 AB=6cm,线段 BC=8cm,则线段 AC 的长度为( )
A. 14cm B. 2cm C. 14cm或2cm D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,A、C、F、D在同一直线上,AF=DC,AB∥DE,AB=DE.
求证:(1) △ABC≌△DEF;
(2)BC∥EF.

-
科目: 来源: 题型:
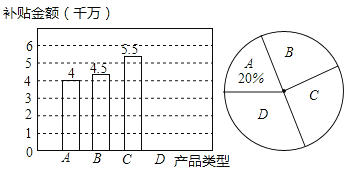
查看答案和解析>>【题目】近几年来,国家对购买新能源汽车实行补助政策,2016年某省对新能源汽车中的“插电式混合动力汽车”实行每辆3万元的补助,小刘对该省2016年“纯电动乘用车”和“插电式混合动力车”的销售计划进行了研究,绘制出如图所示的两幅不完整的统计图.
(1)补全条形统计图;
(2)求出“D”所在扇形的圆心角的度数;
(3)为进一步落实该政策,该省计划再补助4.5千万元用于推广上述两大类产品,请你预测,该省16年计划大约共销售“插电式混合动力汽车”多少辆?
注:R为纯电动续航行驶里程,图中A表示“纯电动乘用车”(100km≤R<150km),B表示“纯电动乘用车”(150km≤R<250km),C表示“纯电动乘用车”(R≥250km),D为“插电式混合动力汽车”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,观察由棱长为
 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有  个小立方体,其中
个小立方体,其中  个看得见,
个看得见,  个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有  个小立方体,其中
个小立方体,其中  个看得见,
个看得见,  个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有  个小立方体,其中
个小立方体,其中  个看得见,
个看得见,  个看不见;
个看不见;  ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.
相关试题

