【题目】如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y= ![]() 与正方形ABCD有公共点,则k的取值范围为( )
与正方形ABCD有公共点,则k的取值范围为( )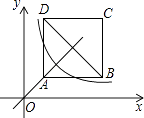
A.1<k<9
B.2≤k≤34
C.1≤k≤16
D.4≤k<16
参考答案:
【答案】C
【解析】∵点A在直线y=x上,横坐标为1,
∴点A的坐标为(1,1),
∵正方形ABCD的边长为3,
∴点C的坐标为(4,4),
当双曲线y= ![]() 经过点A时,k=1×1=1,
经过点A时,k=1×1=1,
当双曲线y= ![]() 经过点C时,,k=4×4=16,
经过点C时,,k=4×4=16,
∴双曲线y=![]()
![]() 与正方形ABCD公共点,则k的取值范围是1≤k≤16,
与正方形ABCD公共点,则k的取值范围是1≤k≤16,
所以答案是:C.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

-
科目: 来源: 题型:
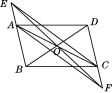
查看答案和解析>>【题目】如图,在ABCD中,点O是AC与BD的交点,过点O的直线与BA的延长线,DC的延长线分别交于点E,F.
(1)求证:△AOE≌△COF.
(2)连接EC,AF,则EF与AC满足什么数量关系时,四边形AECF是矩形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD,其中AD//BC,AB⊥BC,将DC沿DE折叠,C落于
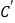 ,
,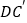 交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点
交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点 (如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.
(如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.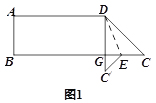
-
科目: 来源: 题型:
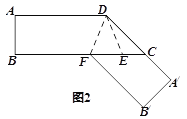
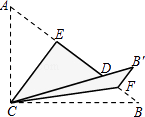
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( )
A.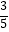
B.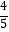
C.
D.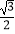
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=30°,∠B=60°,AB⊥AC.
(1)∠DAB+∠B等于多少度?(2)AD与BC平行吗?AB与CD平行吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
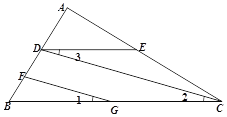
解:∵FG//CD (已知)
∴∠2=_________(____________________________)
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//__________(_____________________________)
∴∠B+________=180°(______________________________)
又∵∠B=50°
∴∠BDE=________________.
相关试题

