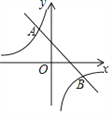
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于点A(m,2),B(2,-1).
的图象交于点A(m,2),B(2,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0),使△ABP为直角三角形,请你直接写出P点的坐标.
参考答案:
【答案】(1)![]() ;y=-x+1;(2)P点的坐标(3,0)、(﹣3,0)、(
;y=-x+1;(2)P点的坐标(3,0)、(﹣3,0)、(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】分析:(1)把点B坐标代入y=![]() 求出反比例函数的解析式,再把点A坐标代入反比例函数的解析式求出m的值,利用待定系数法求出一次函数解析式.
求出反比例函数的解析式,再把点A坐标代入反比例函数的解析式求出m的值,利用待定系数法求出一次函数解析式.
(2)分三种情况进行讨论, ①当∠BAP=90°; ②当∠BPA=90°; ③当∠PBA=90°, 利用勾股定理的逆定理建立方程即可得出结论.
详解: (1)把A(1,2)代入y=![]() 得:2=k 1
得:2=k 1
∴k =2×(1)=2
∴![]()
把B(m,2)代入![]() 得:m=-1,
得:m=-1,
∴B(-1,2)
把A(1,2),B(2,1)分别代入y=k x+b得:
![]()
∴![]()
∴y=x+1
(2)∵A(1,2),B(2,1),P(n,0),
∴AB =18,AP =(n+1) +4,BP =(n2) +1,
∵△ABP为直角三角形,
∴①当∠ABP=90°时,AB +BP =AP ,
∴18+(n2) +1=(n+1) +4,
∴n=3,
∴P(3,0),
②当∠BAP=90°时,AB +AP =BP ,
∴18+(n+1) +4=(n2) +1,
∴n=3,
∴P(3,0),
③当∠APB=90°时,AP +BP =AB ,
∴(n+1) +4+(n2) +1=18,
∴n=![]() ,
,
∴P(![]() ,0)或(
,0)或(![]() ,0)
,0)
即:P点的坐标(3,0)、(3,0)、(![]() ,0)或(
,0)或(![]() ,0).
,0).
点睛: 本题考查反比例函数和一次函数解析式的确定、等腰直角三角形的判定等知识及综合应用知识、解决问题的能力.要注意在不确定直角三角形的直角边和底边的情况下要考虑到所有的情况,不要漏解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(
 ,1)在射线OM上,点B(
,1)在射线OM上,点B( ,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,
,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2, ,依此规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为__.
,依此规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对市区居民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
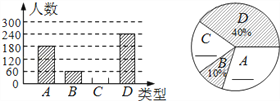
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?并将两幅不完整的图补充完整;
(2)若常德市武陵区居民有60万人口,估计有多少人爱吃肉馅粽?
(3)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
-
科目: 来源: 题型:
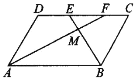
查看答案和解析>>【题目】如图所示,已知四边形ABCD是平行四边形,∠C=70°,若AF、BE分别为∠DAB、∠CBA的平分线.
求证:(1)DF=EC;(2)求∠DFA的大小。
-
科目: 来源: 题型:
查看答案和解析>>【题目】〖定义〗:若关于
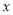 的一元一次方程
的一元一次方程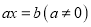 的解恰好为
的解恰好为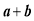 即
即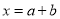 ,则称该方程为“友好方程”.例如:方程
,则称该方程为“友好方程”.例如:方程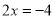 的解为
的解为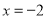 ,而
,而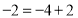 ,则方程
,则方程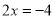 为“友好方程”.
为“友好方程”.〖运用〗:(1)①
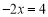 ,②
,②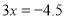 ③
③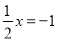 三个方程中,为“友好方程”的是______(填写序号)
三个方程中,为“友好方程”的是______(填写序号)(2)若关于
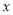 的一元一次方程
的一元一次方程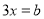 是“友好方程”,求
是“友好方程”,求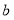 的值;
的值;(3)若关于
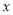 的一元一次方程
的一元一次方程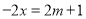 是“友好方程”,求
是“友好方程”,求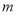 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案。
-
科目: 来源: 题型:
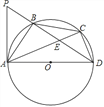
查看答案和解析>>【题目】如图,△ABC内接于⊙O,且AB=BC.AD是⊙O的直径,AC、BD交于点E,P为DB延长线上一点,且PB=BE.
(1)求证:△ABE∽△DBA;
(2)试判断PA与⊙O的位置关系,并说明理由;
(3)若E为BD的中点,求tan∠ADC的值.
相关试题

