【题目】如图,已知![]() 、
、![]() ,
,![]() ,
,![]() 为
为![]() 点关于
点关于![]() 的对称点,反比例函数
的对称点,反比例函数![]() 的图像经过
的图像经过![]() 点.
点.

(![]() )证明四边形
)证明四边形![]() 为菱形.
为菱形.
(![]() )求此反比例函数的解析式.
)求此反比例函数的解析式.
(![]() )已知点
)已知点![]() 在
在![]() 的图像上,点
的图像上,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 、
、![]() 、
、![]() 、
、![]() 组成四边形是平行四边形,求
组成四边形是平行四边形,求![]() 点的坐标.
点的坐标.
参考答案:
【答案】(![]() )证明见解析(
)证明见解析(![]() )
)![]() (
(![]() )
)![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,![]()
【解析】
试题(![]() )先计算出
)先计算出![]() ,
,![]() ,再根据轴对称的性质得
,再根据轴对称的性质得![]() ,
,![]() ,于是可根据菱形的判定方法得到四边形
,于是可根据菱形的判定方法得到四边形![]() 为菱形;
为菱形;
(![]() )由菱形的性质得
)由菱形的性质得![]() ,则
,则![]() ,然后把
,然后把![]() 点坐标代入关系式求出
点坐标代入关系式求出![]() 的值即可得到反比例函数解析式;
的值即可得到反比例函数解析式;
(![]() )讨论:当
)讨论:当![]() 为对角线,利用平行四边形的性质,可把
为对角线,利用平行四边形的性质,可把![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,则
点,则![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,则利用反比例函数解析式可确定
点,则利用反比例函数解析式可确定![]() 坐标,于是得到
坐标,于是得到![]() 点通过平移可得
点通过平移可得![]() 点,利用同样平移得到
点,利用同样平移得到![]() 点坐标,当
点坐标,当![]() 为边,由四边形
为边,由四边形![]() 为平行四边形得到
为平行四边形得到![]() ,
,![]() ,则可确定
,则可确定![]() 坐标,进而可求
坐标,进而可求![]() ,
,![]() 及
及![]() ,易得
,易得![]() 点坐标.
点坐标.
试题解析:(![]() )∵
)∵![]() 、
、![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 为
为![]() 点关于
点关于![]() 的对称点,
的对称点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 为菱形.
为菱形.
(![]() )∵四边形
)∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,
而![]() ,
,![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
∴反比例函数解析式为![]() .
.
(![]() )当
)当![]() 为对角线,如图,
为对角线,如图,
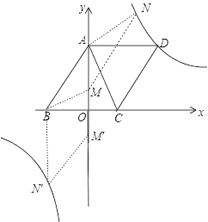
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,
点,![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,
点,
∴![]() 点的横坐标为
点的横坐标为![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
∴![]() 点向右平移
点向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 单位可得
单位可得![]() 点,
点,
∴![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,再向上平移
点,再向上平移![]() 单位可得
单位可得![]() 点,此时
点,此时![]() 点坐标为
点坐标为![]() ;
;
当![]() 为边,
为边,
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]() ,
,
∴![]() 点的横坐标为
点的横坐标为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,或
,或![]() ,
,
此时![]() 点坐标为
点坐标为![]() 或
或![]() ,
,
综上所述,满足条件的![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O为坐标原点.直线y=kx+b与抛物线y=mx2﹣
 x+n同时经过A(0,3)、B(4,0).
x+n同时经过A(0,3)、B(4,0).
(1)求m,n的值.
(2)点M是二次函数图象上一点,(点M在AB下方),过M作MN⊥x轴,与AB交于点N,与x轴交于点Q.求MN的最大值.
(3)在(2)的条件下,是否存在点N,使△AOB和△NOQ相似?若存在,求出N点坐标,不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )
A.极差是6
B.众数是10
C.平均数是9.5
D.方差是16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则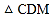 周长的最小值为
周长的最小值为


A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,E是直线l两侧的点,以C为圆心,CE长为半径画弧交l于A,B两点,又分别以A,B为圆心,大于
 AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,下列结论不一定正确的是( )
AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,下列结论不一定正确的是( ) 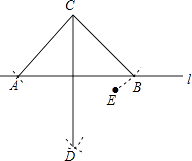
A.CD⊥l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .

相关试题

