【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m=;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n=;
(2)①如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;
(3)该函数的最小值为;
(4)已知直线 ![]() 与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
参考答案:
【答案】
(1)1,﹣10
(2)该函数的图象如图
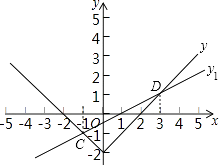
根据函数图象可得:
(3)-2
(4)﹣1≤x≤3
【解析】解:(1)①把x=3代入y=|x|﹣2,得m=3﹣2=1.
所以答案是1;②把y=8代入y=|x|﹣2,得8=|x|﹣2,
解得x=﹣10或10,
∵A(n,8),B(10,8)为该函数图象上不同的两点,
∴n=﹣10.
所以答案是﹣10;
⑵在同一平面直角坐标系中画出函数 ![]() 与函数y=|x|﹣2的图象,
与函数y=|x|﹣2的图象,
⑶该函数的图象如图,①该函数的最小值为﹣2;

所以答案是:(1)①1;②-10;(2)见解答过程;(3)﹣2;⑷﹣1≤x≤3.
【考点精析】根据题目的已知条件,利用一次函数的性质和一次函数的图象和性质的相关知识可以得到问题的答案,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )
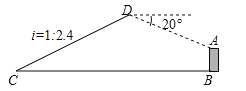
A.29.1米 B.31.9米 C.45.9米 D.95.9米
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数-6、1、-3、5、-2中任取两个数相乘,其中最大的积是______,最小的积是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙,丙,丁四位同学在四次数学测验中,他们成绩的平均数相同,方差分别为S甲2=5.5,S乙2=7.3,S丙2=8.6,S丁2=4.5,则成绩最稳定的是( )
A.甲同学
B.乙同学
C.丙同学
D.丁同学 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=30°,点P在∠AOB内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2的形状一定是( )
A. 直角三角形 B. 等边三角形 C. 底边和腰不相等的等腰三角形 D. 钝角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂今年元月份的产量是50万元,3月份的产值达到了72万元.若求2、3月份的产值平均增长率,设这两个月的产值平均月增长率为x,依题意可列方程( )
A.72(x+1)2=50
B.50(x+1)2=72
C.50(x﹣1)2=72
D.72(x﹣1)2=50 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 分钟到达终点B.

相关试题

