【题目】(2016广东省深圳市第21题)荔枝是深圳特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)
(1)、求桂味和糯米糍的售价分别是每千克多少元;
(2)、如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的两倍,请设计一种购买方案,使所需总费用最低.
参考答案:
【答案】(1)、桂味售价为每千克15元,糯米味售价为每千克20元;(2)、购买桂味4千克,糯米味8千克是,总费用最少.
【解析】
试题分析:(1)、首先设桂味售价为每千克x元,糯米味售价为每千克y元,根据题意列出二元一次方程组,从而求出x和y的值,得出答案;(2)、设购买桂味t千克,总费用为w元,则购买糯米味12-t千克,根据题意得出t的取值范围,然后得出w与t的函数关系式,从而得出最值.
试题解析:(1)、设桂味售价为每千克x元,糯米味售价为每千克y元,根据题意得:![]()
解得:![]()
答:桂味售价为每千克15元,糯米味售价为每千克20元。
(2)、设购买桂味t千克,总费用为w元,则购买糯米味12-t千克, ∴12-t≥2t ∴t≤4
W=15t+20(12-t)=-5t+240. ∵k=-5<0 ∴w随t的增大而减小
∴当t=4时,wmin=220.
答:购买桂味4千克,糯米味8千克是,总费用最少。
-
科目: 来源: 题型:
查看答案和解析>>【题目】时钟在3点半时,分针与时针所夹的角的度数是( )
A. 67.5° B. 75° C. 82.5° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.(1)直接写出m= ,n= ;
(2)根据图象直接写出使kx+b<
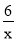 成立的x的取值范围 ;
成立的x的取值范围 ;(3)在x轴上找一点P使PA+PB的值最小,求出P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
某商店能过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:
第1个
第2个
第3个
第4个
…
第n个
调整前单价x(元)
x1
x2=6
x3=72
x4
…
xn
调整后单价x(元)
y1
y2=4
y3=59
y4
…
yn
已知这n个玩具调整后的单价都大于2元.
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为
 ,
, ,猜想
,猜想 与
与 的关系式,并写出推导出过.
的关系式,并写出推导出过. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上A点表示数a,B点表示数b,a、b满足
 +
+ =0;
=0;(1)点A表示的数为_______;点B表示的数为__________;
(2)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①当t=1时,甲小球到原点的距离=_______;乙小球到原点的距离=_______;当t=3时,甲小球到原点的距离=_______;乙小球到原点的距离=_______;
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由。若能,请求出甲,乙两小球到原点的距离相等时经历的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
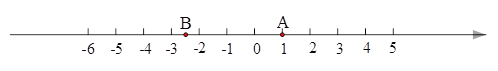
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数
A: ___________ B: _____________ ;
(2)观察数轴,与点A的距离为4的点表示的数是:_____________ ;
(3)若将数轴折叠,使得A点与-3表示的点重合,则B点与数_ _表示的点重合;
(4)若数轴上M、N两点之间的距离为2014(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是: M: _______ N: _______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面截一个几何体,若截面是三角形,则这个几何体可能是__________.
相关试题

