【题目】下列计算正确的是( )
A.x3?x﹣4=x﹣12
B.(x3)3=x6
C.2x2+x=x
D.(3x)﹣2= ![]()
参考答案:
【答案】D
【解析】解:A、同底数幂的乘法底数不变指数相加,故A错误; B、幂的乘方底数不变指数相乘,故B错误;
C、不是同类项不能合并,故C错误;
D、负整数指数幂与正整数指数幂互为倒数,故D正确;
故选:D.
【考点精析】利用整数指数幂的运算性质和同底数幂的乘法对题目进行判断即可得到答案,需要熟知aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数);同底数幂的乘法法则aman=am+n(m,n都是正数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
 、
、 、
、 、
、 分别在矩形
分别在矩形 的边
的边 、
、 、
、 、
、 上,
上,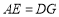 .
.求证:
 .(
.( 表示面积)
表示面积)
实验探究:
某数学实验小组发现:若图1中
 ,点
,点 在
在 上移动时,上述结论会发生变化,分别过点
上移动时,上述结论会发生变化,分别过点 、
、 作
作 边的平行线,再分别过点
边的平行线,再分别过点 、
、 作
作 边的平行线,四条平行线分别相交于点
边的平行线,四条平行线分别相交于点 、
、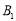 、
、 、
、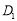 ,得到矩形
,得到矩形 .
.如图2,当
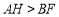 时,若将点
时,若将点 向点
向点 靠近(
靠近( ),经过探索,发现:
),经过探索,发现: .
.如图3,当
 时,若将点
时,若将点 向点
向点 靠近(
靠近( ,请探索
,请探索 、
、 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题.
(1)如图4,点
 、
、 、
、 、
、 分别是面积为25的正方形
分别是面积为25的正方形 各边上的点,已知
各边上的点,已知 ,
, ,
, ,
, ,求
,求 的长.
的长.
(2)如图5,在矩形
 中,
中, ,
, ,点
,点 、
、 分别在边
分别在边 、
、 上,
上, ,
, ,点
,点 、
、 分别是边
分别是边 、
、 上的动点,且
上的动点,且 ,连接
,连接 、
、 ,请直接写出四边形
,请直接写出四边形 面积的最大值.
面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两边b=4,c=7,试确定第三边a的范围.当各边均为整数时,有几个三角形?有等腰三角形吗?等腰三角形的边长各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3+a2=a5
B.a3a2=a6
C.(a2)3=a6
D.a6÷a3=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+2x=0的根是( )
A. 2B. 0C. 0或2D. 0或﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县响应“建设环保节约型社会”的号召,决定资助部分村镇修建一批沼气池,使农民用到经济、环保的沼气能源.幸福村共有264户村民,政府补助村里34万元,不足部分由村民集资.修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用户数、修建用地情况如下表:
沼气池
修建费用(万元/个)
可供使用户数(户/个)
占地面积(m2/个)
A型
3
20
48
B型
2
3
6
政府相关部门批给该村沼气池修建用地708平方米.设修建A型沼气池x个,修建两种型号沼气池共需费用y万元.
(1)用含有x的代数式表示y;
(2)不超过政府批给修建沼气池用地面积,又要使该村每户村民用上沼气的修建方案有几种;
(3)若平均每户村民集资700元,能否满足所需费用最少的修建方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个式子中,是方程的是( )
A.3+2=5B.3x–2=1C.2x–3<0D.a2+2ab+b2
相关试题

