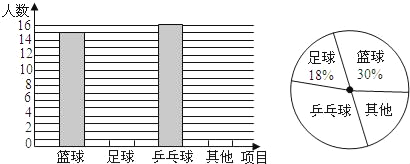
【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有_____名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为_____;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
参考答案:
【答案】 50 见解析(3)115.2° (4)![]()
【解析】试题分析:(1)用最喜欢篮球的人数除以它所占的百分比可得总共的学生数;
(2)用学生的总人数乘以各部分所占的百分比,可得最喜欢足球的人数和其他的人数,即可把条形统计图补充完整;
(3)根据圆心角的度数=360 ×它所占的百分比计算;
(4)列出树状图可知,共有20种等可能的结果,两名同学恰为一男一女的有12种情况,从而可求出答案.
解:(1)由题意可知该班的总人数=15÷30%=50(名)
故答案为:50;
(2)足球项目所占的人数=50×18%=9(名),所以其它项目所占人数=50﹣15﹣9﹣16=10(名)
补全条形统计图如图所示:
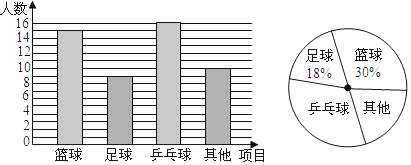
(3)“乒乓球”部分所对应的圆心角度数=360°×![]() =115.2°,
=115.2°,
故答案为:115.2°;
(4)画树状图如图.
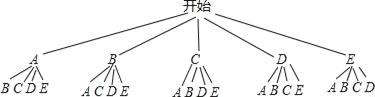
由图可知,共有20种等可能的结果,两名同学恰为一男一女的有12种情况,
所以P(恰好选出一男一女)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A.
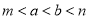 B.
B. 
C.
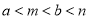 D.
D. 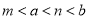
-
科目: 来源: 题型:
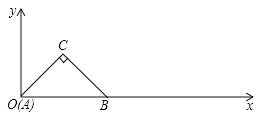
查看答案和解析>>【题目】(3分)在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大正方形内有两个大小一样的长方形ABCD和长方形EFGH,且AB,AD,EF,EH分别在大正方形的四条边上,大正方形内有个小正方形与两长方形有重叠(图中两个长方形形状的阴影部分),若B两正方形的周长分别为44与30,且AB=EH=6,AD=EF=3,则两阴影部分的周长和为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点O在直线PQ上,过点O作射线OC,使∠POC=130°,将一直角三角板的直角顶点放在点O处.
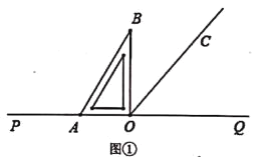
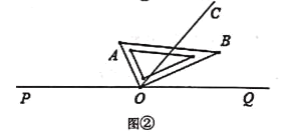
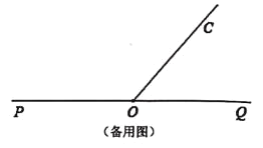
(1)如图①所示,将直角三角板AOB的一边OA与射线OP重合,则∠BOC=________°.
(2)将图①中的直角三角板AOB绕点O旋转一定角度得到如图②所示的位置,若OA平分∠POC,求∠BOQ的度数.
(3)将图①中的直角三角板AOB绕点O旋转一周,存在某一时刻恰有OB⊥OC,求出所有满足条件的∠AOQ的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图:反比例函数y=
 的图象经过点A(﹣3,b)过点A作x轴的垂线,垂足为B,S△AOB=3.
的图象经过点A(﹣3,b)过点A作x轴的垂线,垂足为B,S△AOB=3.(1)求k,b的值;
(2)若一次函数y=ax+1的图象经过点A,且与x轴交于M,求AM的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度是多少?

相关试题

