【题目】如图,经过点A(0,﹣4)的抛物线y=![]() x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.

(1)求抛物线的解析式;
(2)将抛物线y=![]() x2+bx+c向上平移7个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
x2+bx+c向上平移7个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
(3)将x轴下方的抛物线图象关于x轴对称,得到新的函数图象C,若直线y=x+k与图象C始终有3个交点,求满足条件的k的取值范围.
参考答案:
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4(2)
x﹣4(2)![]() <m<
<m<![]() (3)1或
(3)1或![]()
【解析】试题分析:
(1)将A、B两点坐标代入![]() 即可解出
即可解出![]() 的值,从而得到抛物线的解析式;
的值,从而得到抛物线的解析式;
(2)将(1)中所得解析式配方,结合已知条件可得平移所得新抛物线的解析式及其顶点坐标;由A、B、C三点的坐标可求得直线AB、AC的解析式,由顶点分别落在AB和AC上可求得对应的“m”的值,即可得到“m”的取值范围;
(3)如图1,当直线![]() 和新的函数图象C有三个公共点时,直线
和新的函数图象C有三个公共点时,直线![]() 分别处于图中
分别处于图中![]() 的位置上;①由
的位置上;①由![]() 过点B,可求得此时“m”的值;②当直线
过点B,可求得此时“m”的值;②当直线![]() 处以
处以![]() 的位置时,由图可知,此时直线和新的函数图象C在
的位置时,由图可知,此时直线和新的函数图象C在![]() 的范围内有1个公共点,由“一元二次方程根的判别式”可求得此时“m”的值;两者综合即可得到本题答案.
的范围内有1个公共点,由“一元二次方程根的判别式”可求得此时“m”的值;两者综合即可得到本题答案.
试题解析:
(1)∵经过点A(0,﹣4)的抛物线![]() 与x轴相交于点B(﹣1,0),
与x轴相交于点B(﹣1,0),
∴ ,解得:
,解得:  ,
,
∴ 抛物线解析式为![]() ;
;
(2)由(1)知,抛物线解析式为![]() ,
,
∴此抛物线向上平移7个单位长度、再向左平移m(m>0)个单位长度后,所得新抛物线的解析式为: ![]() ,
,
∴新抛物线的顶点P的坐标为![]() ,
,
对于抛物线![]() 当
当![]() 时,有
时,有![]() ,由此解得
,由此解得![]() =﹣1或8,
=﹣1或8,
∴C的坐标为(8,0),
又∵A(0,﹣4),B(﹣1,0),
∴可解得直线AB的解析式为y=﹣4x﹣4,直线AC的解析式为y=![]() x﹣4,
x﹣4,
由此可得:
①当顶点P在AB上时,可得: ![]() ,解得m=
,解得m=![]() ,
,
②当顶点P在AC上时,可得: ![]() ,解得m=
,解得m=![]() ,
,
∴综合①②可得,当点P在△ABC内时m的取值范围是: ![]() ;
;
(3)翻折后所得新图象如图1所示.
当直线![]() 和新图象C(其中翻折所得部分为
和新图象C(其中翻折所得部分为![]() )有三个公共点时,直线
)有三个公共点时,直线![]() 分别处在图中
分别处在图中![]() 的位置上:
的位置上:

①当直线l位于l1时,此时直线![]() 过点B(﹣1,0),
过点B(﹣1,0),
∴0=﹣1+k,解得:k=1;
②∵当直线l位于l2时,此时直线![]() 与函数
与函数![]() 的图象有一个公共点,
的图象有一个公共点,
∴方程![]() ,即
,即![]() 有两个相等实根.
有两个相等实根.
∴△=25﹣4(2k﹣8)=0,即k=![]() .
.
综上所述,k的值为1或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
基本不等式
 ≤
≤ (a>0,b>0),当且仅当a=b时等号成立,它是解决最值问题的有力工具.
(a>0,b>0),当且仅当a=b时等号成立,它是解决最值问题的有力工具.例如:在x>0的条件下,当x为何值时,x+
 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵x>0,
 >0∴
>0∴ ≥
≥ ,即
,即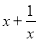 ≥2
≥2 ,∴
,∴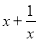 ≥2
≥2当且仅当x=
 ,即x=1时,x+
,即x=1时,x+ 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题:
(1)已知x>0,则当x为____时,代数式3x+
 的最小值为______;
的最小值为______;(2)已知a>0,b>0,a2+b2=7,则ab的最大值为_____
(3)已知矩形面积为9,求矩形周长的最小值.
-
科目: 来源: 题型:
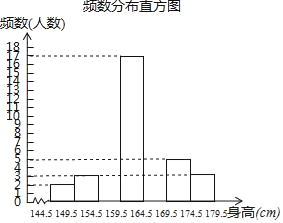
查看答案和解析>>【题目】为了解同学们的身体发育情况,学校体卫办公室对七年级全体学生进行了身高测量(精确到1cm),并从中抽取了部分数据进行统计,请根据尚未完成的频数分布表和频数分布直方图解答下列问题:
频率分布表
分组
频数
百分比
144.5~149.5
2
4%
149.5~154.5
3
6%
154.5~159.5
a
16%
159.5~164.5
17
34%
164.5~169.5
b
n%
169.5~174.5
5
10%
174.5~179.5
3
6%
(1)求a、b、n的值;
(2)补全频数分布直方图;
(3)学校准备从七年级学生中选拔护旗手,要求身高不低于170cm,如果七年级有学生350人,护旗手的候选人大概有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年第37届洛阳牡丹文化节期间龙门石窟旅游景点共接待游客92. 4万人次,和去年同时期相比,游客总数增加了
 ,其中省外游客增加了
,其中省外游客增加了 ,省内游客增加了
,省内游客增加了 .
. (1)求该景点去年牡丹文化节期间接待的省外游客和省内游客各是多少万人?
(2)若省外游客每位门票均价约为100元,省内游客每位门票均价约为80元,则今年文化节期间该景点的门票收入大约是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点为(1,﹣4),且过点(﹣2,5).
(1)求抛物线解析式;
(2)直接写出当函数值y>0时,自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:反比例函数
 的图像过点A(
的图像过点A( ,
, ),B(
),B(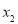 ,
,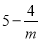 )且
)且
(1)求m的值;
(2)点C在x轴上,且
 ,求C点的坐标;
,求C点的坐标;(3)点Q是第一象限内反比例函数图象上的动点,且在直线AB的右侧,设直线QA,QB与y轴分别交于点E、D,试判断DE的长度是否变化,若变化请说明理由,若不变,请求出长度.
相关试题

