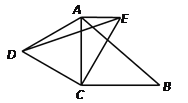
【题目】如图,在△ABC中,∠ ACB=90°BC=2,将△ACB绕点C逆时针旋转60°得到△DCE(A和D,B和E分别是对应顶点),若AE∥BC,则△ADE的周长为_________.
参考答案:
【答案】![]()
【解析】 根据旋转的性质得到CE=BC=2,AC=CD,∠BCE=∠ACD=60°,∠DCE=∠ACB=90°,推出△ACD是等边三角形,得到AD=AC,然后解直角三角形,由勾股定理即可得到结论.
∵将△ACB绕点C逆时针旋转60°得到△DCE,
∴CE=BC=2,AC=CD,∠BCE=∠ACD=60°,∠DCE=∠ACB=90°,
∴△ACD是等边三角形,
∴AD=AC,
∵AE∥BC,
∴∠EAC=90°,∠AEC=∠BCE=60°,
∴AE=![]() CE=1,AC=CD=
CE=1,AC=CD=![]() CE=
CE=![]() ,
,
∴DE=![]() ,
,
∴△ADE的周长=AE+AC+CE=1+![]() +
+![]() ,
,
故答案为:1+![]() +
+![]() .
.
“点睛”本题考查了旋转的性质,等边三角形的判定和性质,直角三角形的性质,平行线的性质,熟练掌握旋转的性质是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应边之比为( )
A. 3:4B. 3:2C. 9:16D. 2:3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,CF∥AB.
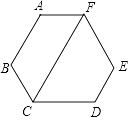
(1)求∠FCD的度数;
(2)求证:AF∥CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】表示“x与4的差的3倍”的代数式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2-8x+15=0,左边化成含有x的完全平方形式,其中正确的是( )
A. x2-8x+(-4)2=31 B. x2-8x+(-4)2=1
C. x2+8x+42=1 D. x2-4x+4=-11
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验探究:
(1)动手操作:
①如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD=;
②如图2,若直角三角板ABC不动,改变等腰直角三角板DEF的位置,使三角板DEF的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD=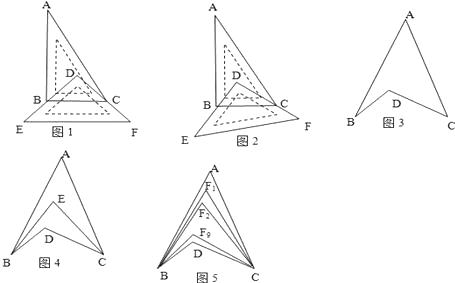
(2)猜想证明:
如图3,∠BDC与∠A、∠B、∠C之间存在着什么关系,并说明理由;
(3)灵活应用:
请你直接利用以上结论,解决以下列问题:
①如图4,BE平分∠ABD,CE平分∠ACB,若∠BAC=40°,∠BDC=120°,求∠BEC的度数;
(4)②如图5,∠ABD,∠ACD的10等分线相交于点F1、F2、…、F9 ,
若∠BDC=120°,∠BF3C=64°,则∠A的度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(x+3)2﹣(x+3)=__.
相关试题

