【题目】(3a-b)(3a+b)-(2a-b)2
参考答案:
【答案】5a2+4ab-2b2
【解析】试题分析:先根据平方差公式与完全平方公式分别计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(2a-b)2=9a2-b2-4a2+4ab-b2=5a2+4ab-2b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
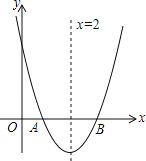
(1)求抛物线的函数表达式;
(2)如果抛物线的对称轴上存在一点P,使得△APC周长的值最小,求此时P点坐标及△APC周长;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是平行四边形,求点D的坐标.(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的周长是20 cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68 cm2,那么矩形ABCD的面积是_______cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小华同学某体育项目7次测试成绩如下(单位:分):9,7,10,8,10,9,10.这组数据的中位数和众数分别为( )
A. 8,10 B. 10,9 C. 8,9 D. 9,10
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各组线段中,不能构成三角形的是( )
A、5,8,10 B、7,10,12 C、4,9,13 D、5,10,13
-
科目: 来源: 题型:
查看答案和解析>>【题目】截至5月21日,全县完成工业开票销售337.53亿元,337.53亿元用科学计数法表示为( )元.
A. 33.753×109 B. 3.3753×1010 C. 0.33753×1011 D. 0.033753×1012
相关试题

