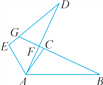
【题目】如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
参考答案:
【答案】90°;65°
【解析】试题分析:根据全等三角形的性质可得∠BAC=∠DAE,根据三角形的内角和定理求出∠BAC,再求出∠BAD,然后根据三角形的一个外角等于与它不相邻的两个内角的和分别求解即可.
试题解析:
∵△ABC≌△ADE,∴∠BAC=∠DAE.
∵∠EAB=∠BAC+∠DAC+∠DAE,∠DAC=10°,∠EAB=120°,
∴∠BAC=∠DAE=55°.
∴∠BAD=∠CAD+∠BAC=65°.
∵∠DFB是△ABF的一个外角,
∴∠DFB=∠BAF+∠B=65°+25°=90°.
又∵∠DFB是△DFG的一个外角,
∴∠DFB=∠D+∠DGB,
∴∠DGB=∠DFB-∠D=90°-25°=65°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据江阴市政府透露江阴市长居人口约1620000人,这个数用科学记数法表示正确的为( )
A. 1.62×102 B. 16.2×10 C. 1.62×106 D. 1.62×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4-m2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
求证:(1)、D是BC的中点;(2)、△BEC∽△ADC;(3)、若
 ,求⊙O的半径。
,求⊙O的半径。
-
科目: 来源: 题型:
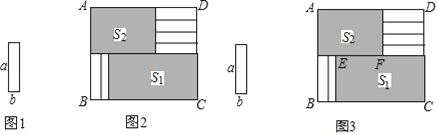
查看答案和解析>>【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.
(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1= ,S2= ;
(2)求a,b满足的关系式,写出推导过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
已知3a-2的算术平方根是4,2a+b-2的算术平方根是3,求a、b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂一周生产自行车7x辆,平均每天生产x辆,但由于种种原因,实际每天生产量与计划产量相比有出入,下表是某周的生产情况(超产记为正,减产记为负。)
星期
一
二
三
四
五
六
日
增产
+5
-2
-4
+13
-10
+16
-8
(1)根据记录的数据可知该厂星期四生产自行车________辆,星期五生产自行车_______辆。
(2)根据记录的数据可知该厂本周实际生产自行车_________辆。
(3)产量最多的一天比产量最少的一天多生产______辆。
(4)若x=300,该厂实行每周计件工资制,每生产一辆自行车,可得60元,若超额完成任务,则超过部分每辆另奖20元,若未完成任务,每少生产一辆扣10元,那么该厂工人这一周的工资总额是多少元?
相关试题

