搜索
【题目】若一次函数y=kx+b的自变量的取值范围是-3≤x≤6，则相应函数值的取值范围是-5≤y≤-2，这个函数的解析式为 .
参考答案：
【答案】
【解析】
试题分析：根据一次函数的增减性，可知本题分两种情况：①当k＞0时，y随x的增大而增大，把x=-3，y=-5；x=6，y=-2代入一次函数的解析式y=kx+b，运用待定系数法即可求出函数的解析式；②当k＜0时，y随x的增大而减小，把x=-3，y=-2；x=6，y=-5代入一次函数的解析式y=kx+b，运用待定系数法即可求出函数的解析式．
分两种情况：
①当k＞0时，把x=-3，y=-5；x=6，y=-2代入一次函数的解析式y=kx+b，
得
解得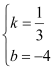
，
则这个函数的解析式是
；
②当k＜0时，把x=-3，y=-2；x=6，y=-5代入一次函数的解析式y=kx+b，
得
解得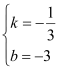
，
则这个函数的解析式是
；
故这个函数的解析式是或
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知平面直角坐标系xOy(如图)，直线 y＝
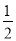x＋b经过第一、二、三象限，与y轴交于点B，点A(2，t)在直线y＝
x＋b上，连结AO，△AOB的面积等于1.(1)求b的值；
(2)如果反比例函数y＝
(k是常量，k≠0)的图象经过点A，求这个反比例函数的表达式．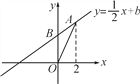
-
科目： 来源： 题型：
查看答案和解析>>【题目】(12分)(2017·黄冈)已知：如图，一次函数y＝－2x＋1与反比例函数y＝
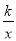的图象有两个交点A(－1，m)和B，过点A作AE⊥x轴，垂足为E；过点B作BD⊥y轴，垂足为点D，且点D的坐标为(0，－2)，连结DE.(1)求k的值；
(2)求四边形AEDB的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，动点P从点A开始沿A→B→C→D 的路径匀速前进到D为止．在这个过程中，△APD的面积S随时间t的变化关系用图象表示正确的是( )
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司仓库本周内货物进出的吨数记录如下
“
”表示进库，“
”表示出库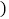
；日期
星期日
星期一
星期二
星期三
星期四
星期五
星期六
吨数
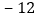
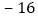
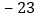
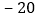
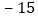
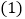这一周，仓库内货物的总吨数是______了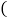填“增多”或“减少”；若周六结束时仓库内还有货物360吨，则周日开始时仓库内有货物多少吨？
如果该仓库货物进出的装卸费都是每吨5元，那么这一周内共需付多少元的装卸费？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某出租车沿公路左右行驶，向左为正，向右为负，某天从A地出发后到收工回家所走的路线如下：
单位：千米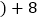
，
，
，
，
，
，
，
，，
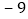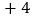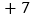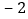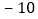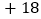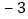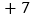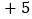
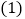问收工时离出发点A多少千米？
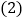若该出租车每千米耗油
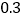升，问从A地出发到收工共耗油多少升？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入
表是某周的生产情况
超产为正、减产为负
： 星期
一
二
三
四
五
六
日
增减
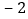
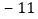
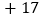
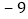
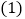根据记录可知前三天共生产多少辆；
产量最多的一天比产量最少的一天多生产多少辆；
该厂实行每周计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？
相关试题
