【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.

参考答案:
【答案】(1)证OE=OC,OF=OC,推出OE=OF,
(2)当点O运动到AC的中点时,四边形AECF是矩形
【解析】试题分析:
(1)先判断∠ECF=90°,再利用角平分线,平行线,等腰三角形的关系得到OE=OC,OF=OC;
(2)结合(1)中的结论,利用对角线相等的平行四边形是矩形说明.
试题解析:
(1)OE=OF,理由如下:
∵CE,CF分别是∠ACB和∠ACB外角的平分线,
∴∠ACE=∠BCE=![]() ∠ACB,∠ACF=∠GCF=
∠ACB,∠ACF=∠GCF=![]() ∠ACG.
∠ACG.
∴∠ECF=∠ACE+∠ACF=![]() ∠ACB+
∠ACB+![]() ∠ACG=
∠ACG=![]() (ACB+∠ACG)=
(ACB+∠ACG)=![]() ∠BCG=90°.
∠BCG=90°.
∵MN∥BC,∴∠FEC=∠BCE,∴∠FEC=∠ACE,∴OE=OC.
同理OF=OC,所以OE=OF.
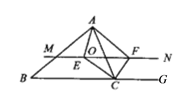
(2)由(1)得,OC=OE=OF,所以当OA=OC时,对角线AC与EF互相平分且相等,而对角线相等的平行四边形是矩形,则当点O运动到AC的中点时,四边形AECF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF

(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE=
 ,求□ABCD的面积.
,求□ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,3),C(5,0).
(1)当α=60°时,△CBD的形状是 _________ ;
(2)当0°<α<90°旋转过程中,连结OH,当△OHC为等腰三角形时,请直接写出点H的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两工程队同时修筑水渠,且两队所修水渠总长度相等.如图是两队所修水渠长度y(米)与修筑时间x(时)的函数图象的一部分.请根据图中信息,解答下列问题:
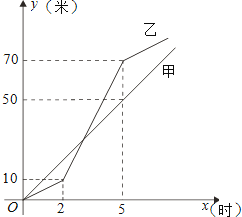
(1)①直接写出甲队在0≤x≤5的时间段内,y与x之间的函数关系式;
②直接写出乙队在2≤x≤5的时间段内,y与x之间的函数关系式;
(2)求开修几小时后,乙队修筑的水渠长度开始超过甲队?
(3)如果甲队施工速度不变,乙队在修筑5小时后,施工速度因故减少到5米/时,结果两队同时完成任务,求乙队从开修到完工所修水渠的长度为多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算与化简.
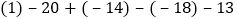
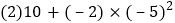
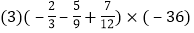
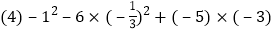
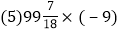
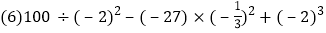 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段BD、CE交于点M.
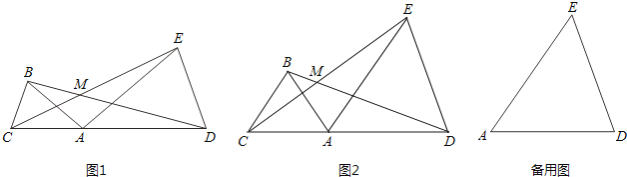
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;
②求∠BMC的大小(用α表示);
(2)如图2,若AB=BC=kAC,AD=ED=kAE,则线段BD与CE的数量关系为 , ∠BMC=(用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接EC并延长交BD于点M.则∠BMC=(用α表示).
相关试题

