搜索
【题目】果园要将批水果运往某地，打算租用某汽车运输公司的甲、乙两种货车．以前两次租用这两种货车的信息如表所示:
第一次 | 第二次 | |
甲种货车车辆数(辆) |
|
|
乙种货车车辆数(辆) |
|
|
累计货运量(吨) |
|
|
（1）甲、乙两种货车每辆每次可分别运水果多少吨？
（2）果园现从该汽车运输公司租用甲、乙两种货车共
辆，要求一次运 送这批水果不少于
吨．请你通过计算，求出果园这次至少租用甲种货车多少辆？
参考答案：
【答案】（1）甲种货车每辆每次可运水果
吨，乙种货车每辆每次可运水果
吨；（2）果园这次至少租用甲种货车辆．
【解析】
（1）设甲、乙两种货车每辆每次可分别运水果x吨、y吨，根据表格中数据进而得出等式求出答案；
（2）利用甲、乙两种货车共8辆，要求一次运送这批水果不少于26吨得出不等关系进而得出答案．
解:
设甲、乙两种货车每辆每次可分别运水果
吨、
吨．
根据题意，得
解这个方程组，得
经检验，方程组的解符合题意．
答:甲种货车每辆每次可运水果吨，乙种货车每辆每次可运水果吨．
设果园这次租用甲种货车
辆，则租用乙种货车
辆．根据题意，得
解这个不等式得
所以，果园这次至少租用甲种货车辆．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=ax2+bx+c（a＜0）的对称轴为x=1，交x轴的一个交点为（x1，0），且﹣1＜x1＜0，有下列5个结论：①abc＞0；②9a﹣3b+c＜0；③2c＜3b；④（a+c）2＜b2；⑤a+b＞m（am+b）（m≠1的实数）其中正确的结论有（ ）
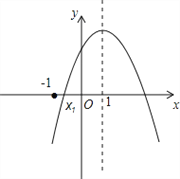
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平面直角坐标系中，已知点A（-3，3），B（-5，1），C（-2，0），P（a，b）是△ABC的边AC上任意一点，△ABC经过平移后得到△A1B1C1，点P的对应点为P1（a+6，b-2）．
（1）直接写出点A1，B1，C1的坐标．
（2）在图中画出△A1B1C1．
（3）连接AA1，求△AOA1的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，抛物线y=x2经过平移得到抛物线y=x2﹣2x，其对称轴与两抛物线所围成的阴影部分的面积是__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学完二元一次方程组的应用之后，老师写出了一个方程组如下：
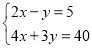，要求把这个方程组赋予实际情境．小军说出了一个情境：学校有两个课外小组，书法组和美术组，其中书法组的人数的二倍比美术组多5人，书法组平均每人完成了4幅书法作品，美术组平均每人完成了3幅美术作品，两个小组共完成了40幅作品，问书法组和美术组各有多少人？
小明通过验证后发现小军赋予的情境有问题，请找出问题在哪？
-
科目： 来源： 题型：
查看答案和解析>>【题目】诗词是我国古代文化中的瑰宝，某市教育主管部门为了解本市初中生对诗词的学习情况，举办了一次“中华诗词”背诵大赛，随机抽取了部分同学的成绩(x为整数，总分100分)，绘制了如下尚不完整的统计图表．
组别
成绩分组(单位：分)
频数
A
50≤x＜60
40
B
60≤x＜70
a
C
70≤x＜80
90
D
80≤x＜90
b
E
90≤x＜100
100
合计
c
根据以上信息解答下列问题：
(1)统计表中a＝ ，b＝ ，c＝ ；
(2)扇形统计图中，m的值为 ，“E”所对应的圆心角的度数是 (度)；
(3)若参加本次大赛的同学共有4000人，请你估计成绩在80分及以上的学生大约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，点C在∠AOB的一边OA上，过点C的直线DE∥OB，CF平分∠ACD，CG⊥CF于点C．
(1)若∠O＝40°，求∠ECF的度数；
(2)求证：CG平分∠OCD．
相关试题
