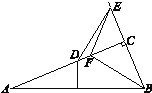
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.

参考答案:
【答案】DE=BF,DE⊥BF.理由见解析.
【解析】试题分析:本题首先要给出答案,在说明理由. 连接DB,根据DH是AB的垂直平分线得出∠A=∠DBH,再根据三角形外角的性质得出∠CDB=∠A+∠DBH,故可得出CD=CB.由SAS定理得出△ECD≌△FCB,所以ED=FB,∠DEC=∠BFC,∠DEC+∠FBC=90°,进而可得出结论.
试题解析:
DE=BF,DE⊥BF.
理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,∴AD=BD,
∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,
∴∠CBD=∠ABC-∠ABD=45°,
∴△BCD为等腰直角三角形,
∴BC=DC.
又∵CE=CF,∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
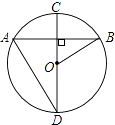
A.AD=AB
B.∠BOC=2∠D
C.∠D+∠BOC=90°
D.∠D=∠B -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE.其中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的顶点B在反比例函数
 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( ) 
A.12
B.4
C.12-3
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了平面直角坐标系及格点△AOB.(顶点是网格线的交点)

(1)画出将△AOB沿y轴翻折得到的△AOB1,则点B1的坐标为_________.
(2)画出将△AOB沿射线AB1方向平移2.5个单位得到的△A2O2B2,则点A2的坐标为_______.
(3)请求出△AB1B2的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红岭中学在“五四青年节”组织九年级全体学生320人进行了一次“爱我中华”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如下频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
分数段(x表示分数)
频数
频率
50≤x<60
4
0.1
60≤x<70
8
b
70≤x<80
a
0.3
80≤x<90
10
0.25
90≤x<100
6
0.15

(1)表中a= , b= , 并补全直方图.
(2)若用扇形统计图描述此成绩分布情况,则分数段60≤x<70对应扇形的圆心角度数是;
(3)请估计该年级分数在80≤x<100的学生有多少人?
相关试题

