【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20![]() 时,按2元/
时,按2元/![]() 计算;月用水量超过20
计算;月用水量超过20![]() 时,其中的20
时,其中的20![]() 仍按2元/
仍按2元/![]() 计算,超过部分按2.6元/
计算,超过部分按2.6元/![]() 计算. 设某户家庭月用水量
计算. 设某户家庭月用水量![]()
![]() .
.

(1)用含![]() 的式子表示:
的式子表示:
当0≤![]() ≤20时,水费为 元;
≤20时,水费为 元;
当![]() >20时,水费为 元.
>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
参考答案:
【答案】(1)2x,(2.6x-12);(2)小花家这个季度共缴纳水费114.4元.
【解析】试题分析:(1)根据水费=单价×数量计算即可;当0≤![]() ≤20时,水费为2x元;当
≤20时,水费为2x元;当![]() >20时,
>20时,
水费为2×20+2.6(x-20);
(2)因4、5月份用水量不超过20m3,所以代入2x求值;因5月份用水量超过20m3,所以代入2.6x-12求值,然后把三个月的水费相加.
解:(1)当0≤![]() ≤20时,水费为 2x___元;
≤20时,水费为 2x___元;
当![]() >20时,水费为 (2.6x-12)__元.
>20时,水费为 (2.6x-12)__元.
(2)15×2+17×2+2.6×24-12= 30+34+62.4-12= 114.4 ,
答:小花家这个季度共缴纳水费114.4元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M的坐标为(1,-2),线段MN=4,MN∥x轴,点N在第三象限,则点N的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,抛物线y=﹣
 x2﹣
x2﹣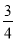 x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
(1)求出直线AD的解析式;
(2)如图2,若在直线AC上方的抛物线上有一点F,当△ADF的面积最大时,有一线段MN=
 (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;(3)如图3,将△DBC绕点D逆时针旋转α°(0<α°<180°),记旋转中的△DBC为△DB′C′,若直线B′C′与直线AC交于点P,直线B′C′与直线DC交于点Q,当△CPQ是等腰三角形时,求CP的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.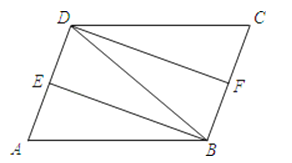
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(1)当∠E=∠F时,则∠ADC=_____°;
(2)当∠A=55°,∠E=30°时,求∠F的度数;
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两相似三角形面积之比为1:4,则它们的周长之比为 ( )
A.1:4B.1:16C.1:2D.1:8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县政府打算用25000元用于为某乡福利院购买每台价格为2000元的彩电和每台价格为1800元的冰箱,并计划恰好全部用完此款.
(1)问原计划所购买的彩电和冰箱各多少台?
(2)由于国家出台“家电下乡”惠农政策,该县政府购买的彩电和冰箱可获得13%的财政补贴,若在不增加县政府实际负担的情况下,能否多购买两台冰箱?谈谈你的想法.
相关试题

