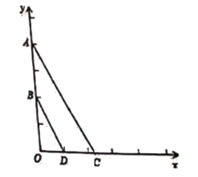
【题目】已知:如图,平面直角坐标系中,![]() ,
,![]() ,点C是x轴上一点,点D为OC的中点.
,点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于2,求点C的坐标;
(3)如果![]() 于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
参考答案:
【答案】(1)BD∥AC;(2) ;(3)
;(3)![]()
【解析】
(1)由A与B的坐标求出OA与OB的长,进而得到B为OA的中点,而D为OC的中点,利用中位线定理即可得证;
(2)如图1,作BF⊥AC于点F,取AB的中点G,确定出G坐标,由平行线间的距离相等求出BF的长,在直角三角形ABF中,利用斜边上的中线等于斜边的一半求出FG的长,进而确定出三角形BFG为等边三角形,即∠BAC=30°,设OC=x,则有AC=2x,利用勾股定理表示出OA,根据OA的长求出x的值,即可确定出C坐标;
(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,进而得到DE垂直于OC,再由D为OC中点,得到OE=CE,再由OE垂直于AC,得到三角形AOC为等腰直角三角形,求出OC的长,确定出C坐标,设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出AC解析式.
(1)![]() ,
,![]() ,
,
![]() ,
,![]() ,点B为线段OA的中点,
,点B为线段OA的中点,
![]() 点D为OC的中点,即BD为
点D为OC的中点,即BD为![]() 的中位线,
的中位线,
![]() ;
;
(2)如图1,作![]() 于点F,取AB的中点G,则
于点F,取AB的中点G,则![]() ,
,
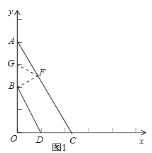
![]() ,BD与AC的距离等于2,
,BD与AC的距离等于2,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,点G为AB的中点,
,点G为AB的中点,
![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() .
.
![]() ,
,
设![]() ,则
,则![]() ,
,
根据勾股定理得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 点C在x轴的正半轴上,
点C在x轴的正半轴上,
![]() 点C的坐标为
点C的坐标为 ;
;
(3)如图2,当四边形ABDE为平行四边形时,![]() ,
,

![]() ,
,
![]() 点D为OC的中点,
点D为OC的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 点C在x轴的正半轴上,
点C在x轴的正半轴上,
![]() 点C的坐标为
点C的坐标为![]() ,
,
设直线AC的解析式为![]() .
.
将![]() ,
,![]() 得
得
![]() ,
,
解得:![]() .
.
![]() 直线AC的解析式为
直线AC的解析式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数y=-2x+4,下列结论错误的是( )
A. 函数的图象与x轴的交点坐标是
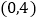
B. 函数值随自变量的增大而减小
C. 函数的图象不经过第三象限
D. 函数的图象向下平移4个单位长度得
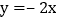 的图象
的图象 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明家、公交车站、学校在一条笔直的公路旁(小明家、学校到这条公路的距离忽略不计),一天,小明从家出发去上学,沿这条公路步行到公交车站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小明下车时发现还有4分钟上课,于是他沿这条公路跑步赶到学校(上、下车时间忽略不计),小明与家的距离s(单位:米)与他所用时间t(单位:分钟)之间的函数关系如图所示,已知小明从家出发7分钟时与家的距离为1200米,从上公交车到他到达学校共用10分钟,下列说法:
①小明从家出发5分钟时乘上公交车 ②公交车的速度为400米/分钟
③小明下公交车后跑向学校的速度为100米/分钟 ④小明上课没有迟到
其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:
 ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)图①中
 的值为 ;
的值为 ;(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为
 的约有多少只?
的约有多少只? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,点E、F、G分别为边AB、BC、CD的中点,若△EFG的面积为4,则四边形ABCD的面积为( )
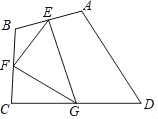
A. 8 B. 12 C. 16 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人玩“石头、剪刀、布”游戏,他们在不透明的袋子中放入形状、大小均相同的12张卡片,其中写有“石头”“剪刀”“布”的卡片张数分别为3、4、5,两人各随机摸出一张卡片(先摸者不放回卡片)来比胜负,并约定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,但同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他摸出哪种卡片获胜的可能性最大?
相关试题

