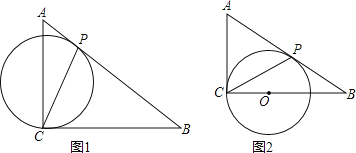
【题目】如图1,Rt△ACB中,AC=3,BC=4,有一动圆⊙O始终与Rt△ACB的斜边AB相切于动点P,且⊙O始终经过直角顶点C.
(1)如图2,当⊙O 运动至与直角边AC相切时,求此时⊙O 的半径r的长;
(2)试求⊙O 的半径r的最小值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由勾股定理先求出AB的值,根据切线长定理得出AP=AC,求出BP的长,再利用△ACB∽△OPB对应边成比例得出圆的半径.
(2)先作出⊙O最大半径时的图,结合三角函数计算r的值.
(1)连接OP,
在Rt△ACB中,AC=3,BC=4,
∴AB=![]() =
=![]() =5,
=5,
∵AC,AP都是圆的切线,
∴AP=AC=3,
∴PB=2,
∵∠ACB=∠OPB=90°,∠B=∠B,
∴△ACB∽△OPB,
∴![]() ,
,
∴![]() ,
,
∴r=![]() .
.
(2)如图,当点P与点B重合时,⊙O的半径最大,此时点O在BC的垂直平分线上,
过点O作OD⊥BC于点D,则BD=![]() BC,
BC,
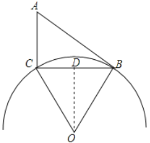
∵AB是切线,
∴∠ABO=90°,
∴∠ABC+∠OBD=∠BOD+∠OBD=90°,
∴∠ABC=∠BOD,
∴sin∠BOD= sin∠ABC=![]() =
=![]() =
=![]() ,
,
∴OB=![]() ,
,
即半径的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块三角形纸板ABC,∠ACB=90°,AC=3,AB=5,把它置于平面直角坐标系中,如图所示.AC∥y轴,BC∥x轴,顶点A,B恰好都在反比例函数y=
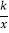 的图象上,AC,BC的延长线分别交x轴、y轴于D,E两点,设点C的坐标为(m,n).
的图象上,AC,BC的延长线分别交x轴、y轴于D,E两点,设点C的坐标为(m,n).(1)求A,B两点的坐标(含m,n,不含k);
(2)当m=n+0.5时,求该反比例函数的解析式.

-
科目: 来源: 题型:
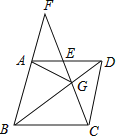
查看答案和解析>>【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加
 kΩ.
kΩ.(1)求当10≤t≤30时,R和t之间的关系式;
(2)求温度在30℃时电阻R的值;并求出t≥30时,R和t之间的关系式;
(3)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过6 kΩ?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(1,yA),B(0,yB),C(-1,yC),D(x1,yD)(x1≠1)在抛物线
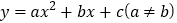 上,且AD//BC,AA1
上,且AD//BC,AA1 轴于A1,DF⊥AAl于F,CE⊥
轴于A1,DF⊥AAl于F,CE⊥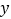 轴于E.
轴于E.(1)求证:△ADF∽△BCE;
(2)当
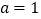 ,
, ,
,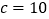 时,求
时,求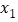 的值;
的值;(3)
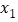 的值会随a,b,c的值改变而改变吗?若会,请求出
的值会随a,b,c的值改变而改变吗?若会,请求出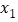 与a,b,c的关系式;若不会,请说明理由.
与a,b,c的关系式;若不会,请说明理由.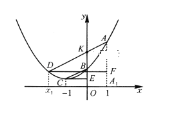
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列语句中,叙述正确的个数为( )
①相等的圆周角所对弧相等;
②同圆等圆中,同弦或等弦所对圆周角相等;
③平分弦的直径垂直于弦;
④等弧所对圆周角相等;
⑤圆的内接平行四边形是矩形;
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为
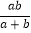 的是( )
的是( )A.
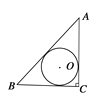 B.
B. 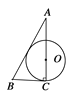 C.
C. 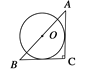 D.
D. 
相关试题

