【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离s (km)与甲车行驶的时间t(h)之间的函数关系如图所示.
(1)请分别求出甲、乙两车离开A城的距离s (km)与甲车行驶的时间t(h)之间的函数表达式;
(2)当甲乙两车都在行驶过程中时,甲车出发多长时间,两车相距50千米.

参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]()
【解析】试题分析:(1)根据图象中的信息分别求出甲乙两车对应的函数解析式;(2)根据(2)中的函数解析式,可知它们相遇前和相遇后两种情况相距50千米,从而可以解答本题.
试题解析:
(1)设甲车离开A城的距离![]() 与甲车行驶的时间t之间的函数表达式为
与甲车行驶的时间t之间的函数表达式为
![]() (
(![]() ≠0)
≠0)
根据题意得:300=5![]() ,
,
∴![]() =60,
=60,
∴甲车离开A城的距离![]() 与甲车行驶的时间t之间的函数表达式为
与甲车行驶的时间t之间的函数表达式为![]() .
.
设乙车离开A城的距离![]() 与甲车行驶的时间t之间的函数表达式为
与甲车行驶的时间t之间的函数表达式为![]() ,
,
根据题意得: ![]()
解得![]()
∴乙车离开A城的距离![]() 与甲车行驶的时间t之间的函数表达式为
与甲车行驶的时间t之间的函数表达式为![]()
(2)由题意得: ![]() ,
,![]()
解得: ![]() ,
, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学去划船,若每船坐7人,则余下5人没有座位;若每船坐8人,则又空出2个座位.这个班参加划船的同学人数和船数分别是( )
A.47,6
B.46,6
C.54,7
D.61,8 -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016云南省第23题)有一列按一定顺序和规律排列的数:
第一个数是
 ;
;第二个数是
 ;
;第三个数是
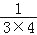 ;
;…
对任何正整数n,第n个数与第(n+1)个数的和等于
 .
.(1)经过探究,我们发现:


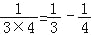
设这列数的第5个数为a,那么
 ,
, ,
, ,哪个正确?
,哪个正确?请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于
 ”;
”;(3)设M表示
 ,
, ,
, ,…,
,…, ,这2016个数的和,即
,这2016个数的和,即 ,
,求证:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a>0,b<﹣2,则点(a,b+2)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 与x轴、y轴相交于P、Q两点,与y=
与x轴、y轴相交于P、Q两点,与y= 的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+
的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+ n=0; ③S△AOP= S△BOQ;④不等式k1x+b>
n=0; ③S△AOP= S△BOQ;④不等式k1x+b> 的解集是x<-2或0<x<1,其中正确的结论的序号是 .
的解集是x<-2或0<x<1,其中正确的结论的序号是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第1个等式:a1=
 =
= ×(1﹣
×(1﹣ );
); 第2个等式:a2=
 =
= ×(
×( ﹣
﹣ );
);第3个等式:a3=
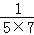 =
= ×(
×( ﹣
﹣ );
); 第4个等式:a4=
 =
= ×(
×( ﹣
﹣ );
);…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
相关试题

