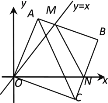
【题目】在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点。现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为________
参考答案:
【答案】4.
【解析】
利用全等把△MBN的各边整理到成与正方形的边长有关的式子即可.
解:如图所示:延长BA交y轴于E点,
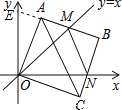
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN,
在△OAE和△OCN中,
∠EOA=∠CON,OA=OC,∠OAE=∠OCN,
,
∴△OAE≌△OCN(ASA).
∴OE=ON,AE=CN.
在△OME和△OMN中,
OE=OC,∠EOM=∠COM,OM=OM,
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
∴△MBN的周长=MN+BN+BM=AM+CN+BN+BM=AB+BC=6.
“点睛”此题主要考查了旋转的性质以及全等三角形的判定与性质等知识,注意求一些线段的长度或角的度数,总要整理到已知线段的长度上或已知角的度数上进而得出是解题关键.
-
科目: 来源: 题型:
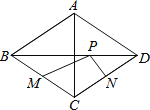
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 ____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能比较
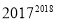 与
与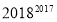 的大小吗?为了解决这个问题,先把问题一般化.即比较
的大小吗?为了解决这个问题,先把问题一般化.即比较 与
与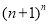 的大小(整数n≥1).然后,从分析n=1,n=2, n=3,……这些简单情形入手,从中发现规律,经过归纳、猜想,得出结论.
的大小(整数n≥1).然后,从分析n=1,n=2, n=3,……这些简单情形入手,从中发现规律,经过归纳、猜想,得出结论.(1)通过计算,比较下列①到⑥各组中两个数的大小:
①
 ②
②  ③
③
④
 ⑤
⑤ ⑥
⑥
(2)从(1)小题的结果归纳,请猜想
 与
与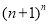 的大小关系:
的大小关系: (3)根据上面归纳猜想到的一般结论,可以得到:
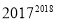 _______
_______ 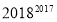 (填“>”、“=”或“<”).
(填“>”、“=”或“<”). -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.


(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是
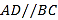 的一张纸条,按图
的一张纸条,按图 图
图 图
图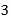 ,把这一纸条先沿
,把这一纸条先沿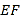 折叠并压平,再沿
折叠并压平,再沿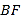 折叠并压平,若图3中
折叠并压平,若图3中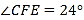 ,则图2中
,则图2中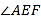 的度数为( )
的度数为( )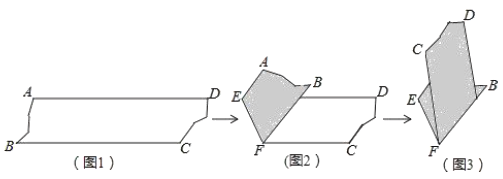
A.
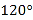 B.
B.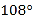 C.
C.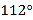 D.
D.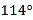
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F是平行四边形ABCD对角线AC上两点,AE=CF.
证明(1)△ABE≌△CDF;
(2)BE∥DF.

相关试题

