【题目】阅读下列一段文字：已知在平面内两点P1（x1，y1）、P2（x2、y2），其两点间的距离P1P2=

问题解决：已知A（1，4）、B（7，2）

（1）试求A、B两点的距离；

（2）在x轴上找一点P（不求坐标，画出图形即可），使PA+PB的长度最短，求出PA+PB的最短长度；

（3）在x轴上有一点M，在Y轴上有一点N，连接A、N、M、B得四边形ANMB，若四边形ANMB的周长最短，请找到点M、N（不求坐标，画出图形即可），求出四边形ANMB的最小周长．

参考答案：

【答案】（1）2；（2）6；（3）10+2．

【解析】

试题分析：（1）根据两点间的距离公式可以解答本题；

（2）根据两点之间线段最短和点的对称可以解答本题；

（3）根据两点之间线段最短和点的对称可以解答本题．

解：（1）∵A（1，4）、B（7，2），

∴AB=

=

=2，

即A、B两点的距离为：2；

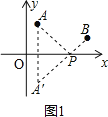
（2）如右图1所示，

作点A关于x轴的对称点A′，

∵A（1，4）、B（7，2），

∴A′（1，﹣4），

∴A′B==6，

即PA+PB的最短长度是6；

（3）作点A关于y轴的对称点A′，作点B关于x轴的对称点B′，连接A′B′于y轴交于点N，与x轴交于点M，如图2所示，

∵A（1，4）、B（7，2），

∴A′（﹣1，4），B′（7，﹣2），

∴AB==2，

A′B′==10，

∴四边形ANMB的最小周长是10+2．

关闭