Question

【题目】如图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE=18°，则图2中∠AEF的度数为（ ）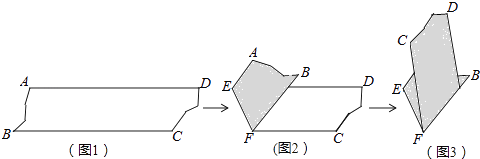
A.108°
B.114°
C.116°
D.120°

Answer 1

【答案】B
【解析】解：如图，设∠B′FE=x， ∵纸条沿EF折叠，
∴∠BFE=∠B′FE=x，∠AEF=∠A′EF，
∴∠BFC=∠BFE﹣∠CFE=x﹣18°，
∵纸条沿BF折叠，
∴∠C′FB=∠BFC=x﹣18°，
而∠B′FE+∠BFE+∠C′FE=180°，
∴x+x+x﹣18°=180°，解得x=66°，
∵A′D′∥B′C′，
∴∠A′EF=180°﹣∠B′FE=180°﹣66°=114°，
∴∠AEF=114°．
故选B．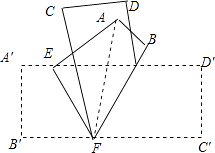

如图，设∠B′FE=x，根据折叠的性质得∠BFE=∠B′FE=x，∠AEF=∠A′EF，则∠BFC=x﹣18°，再由第2次折叠得到∠C′FB=∠BFC=x﹣18°，于是利用平角定义可计算出x=66°，接着根据平行线的性质得∠A′EF=180°﹣∠B′FE=114°，所以∠AEF=114°．