【题目】已知关于x的一元二次方程x2﹣3x+k=0方程有两实根x1和x2.
(1)求实数k的取值范围;
(2)当x1和x2是一个矩形两邻边的长且矩形的对角线长为![]() ,求k的值.
,求k的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题(1)求出△的值,根据已知得出不等式,求出即可;
(2)根据根与系数的关系得出x1+x2=3,x1x2=k,根据已知得出x12+x22=(![]() )2,变形后代入求出即可.
)2,变形后代入求出即可.
试题解析:(1)∵关于x的一元二次方程x2-3x+k=0有两个实根x1和x2,
∴△=(-3)2-4k≥0,
解得:k≤![]() ,
,
即实数k的取值范围为k≤![]() ;
;
(2)由根与系数的关系得:x1+x2=3,x1x2=k,
∵x1和x2是一个矩形两邻边的长且矩形的对角线长为![]() ,
,
∴x12+x22=(![]() )2,
)2,
(x1+x2)2-2x1x2=5,
∴9-2k=5,
解得:k=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场统计了每个营业员在某月的销售额,绘制了如下的条形统计图以及不完整的扇形统计图:
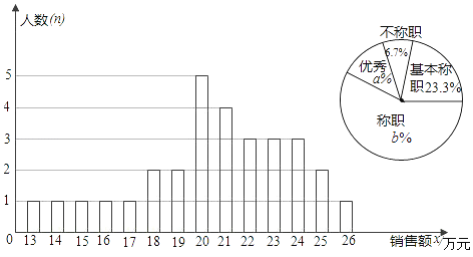
解答下列问题:
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.则扇形统计图中的a=________,b=________.
(2)所有营业员月销售额的中位数和众数分别是多少?
(3)为了调动营业员的积极性,决定制定一个月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得营业员的半数左右能获奖,奖励标准应定为多少万元?并简述其理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年1月25日,上海地区下了一场大雪.这天早上王大爷去买菜,他先去了超市,发现蔬菜普遍涨价了,青菜、花菜和大白菜这两天的价格如下表.王大爷觉得超市的菜不够新鲜,所以他又去了菜市场,他花了30元买了一些新鲜菠菜,他跟卖菜阿姨说:“你今天的菠菜比昨天涨了5元/斤。”卖菜阿姨说:“下雪天从地里弄菜不容易啊,所以你花这些钱要比昨天少买1斤了。”王大爷回答道:“应该的,你们也真的辛苦。”
青菜
花菜
大白菜
1月24日
2元/斤
5元/斤
1元/斤
1月25日
2.5元/斤
7元/斤
1.5元/斤
(1)请问超市三种蔬菜中哪种涨幅最大?并计算其涨幅;
(2)请你根据王大爷和卖菜阿姨的对话,来算算,这天王大爷买了几斤菠菜?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空: a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
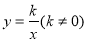 ,在每个象限内y随着x的增大而增大,点P(a-1, 2)在这个反比例函数上,a的值可以是()
,在每个象限内y随着x的增大而增大,点P(a-1, 2)在这个反比例函数上,a的值可以是()A. 0B. 1C. 2D. 3
相关试题

