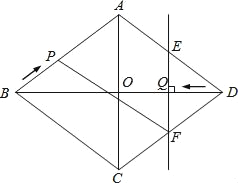
【题目】如图,在菱形ABCD中,AC,BD交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为lcm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为lcm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q.F,当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)求菱形ABCD的面积;
(2)当t=1时,求QF长;
(3)是否存在某一时刻t,使四边形APFD是平行四边形?若存在,求出t值,若不存在,请说明理由;
(4)设△DEF的面积为s(cm2),试用含t的代数式表示S,并求t为何值时,△DEF的面积与△BPC的面积相等.
参考答案:
【答案】(1)96(cm2);(2)![]() ;(3)当t=
;(3)当t=![]() s时,四边形APFD是平行四边形.(4)S=
s时,四边形APFD是平行四边形.(4)S=![]() t2,当t=
t2,当t=![]() 时,△DEF的面积与△BPC的面积相等
时,△DEF的面积与△BPC的面积相等
【解析】
菱形面积=![]() ×AC×BD;
×AC×BD;
由EF∥AC,可得![]() ,即可求QF的长;
,即可求QF的长;
(3)当AP=DF时,四边形APFD为平行四边形,用t表示出AP=10-t,DF=
![]() t,列等式计算;
t,列等式计算;
(4)用t表示出△DEF和△BPC的面积,令其相等,即可求.
解:(1)∵四边形ABCD是菱形,AC=12cm,BD=16cm,
∴菱形ABCD的面积为![]() ×12×16=96(cm2).
×12×16=96(cm2).
(2)∵AB∥CD,AC⊥BD,OA=OC=6cm,OB=OD=8cm,
在![]() 中,AB=
中,AB=![]() (cm),
(cm),
当t=1时,DQ=1,
∵EF⊥BD,AC⊥BD,
∴EF∥AC,
∴![]() ,
,
∴![]() ,
,
∴QF=![]() (cm).
(cm).
(3)∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,OA=OC=6,OB=OD=8.
在![]() 中,AB=
中,AB=![]() .
.
∵EF⊥BD,
∴∠FQD=∠COD=90°.
又∵∠FDQ=∠CDO,
∴△DFQ∽△DCO.
∴![]() ,
,
即![]() ,
,
∴DF=![]() t.
t.
∵四边形APFD是平行四边形,
∴AP=DF.
即10﹣t=![]() t,
t,
解这个方程,得t=![]() .
.
∴当t=![]() s时,四边形APFD是平行四边形.
s时,四边形APFD是平行四边形.
(4)S=S△DEF=![]() .
.
如图作CG⊥AB于点G.
∵S菱形ABCD=ABCG=![]() ACBD,
ACBD,
即10CG=![]() ×12×16,
×12×16,
∴CG=![]() ,
,
∴S△BPC=![]() t×
t×![]() =
=![]() t,
t,
当△DEF的面积与△BPC的面积相等时,
![]() ,
,
解得t=![]() 或t=0(舍弃),
或t=0(舍弃),
∴S=![]() ,当t=
,当t=![]() 时,△DEF的面积与△BPC的面积相等
时,△DEF的面积与△BPC的面积相等
-
科目: 来源: 题型:
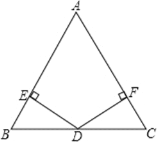
查看答案和解析>>【题目】如图,在
 中,
中,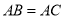 ,点
,点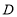 是
是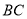 边上的中点,
边上的中点,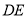 、
、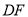 分别垂直
分别垂直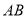 、
、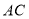 于点
于点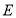 和
和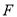 .求证:
.求证: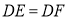
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料阅读:
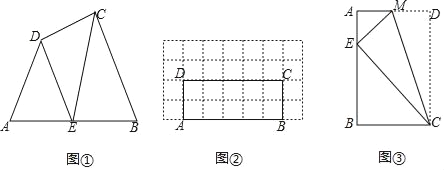
如图①,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点(无需写解答过程);
(3)如图③所示的矩形ABCD,将矩形ABCD沿CM折叠后,点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究点E的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)|﹣3|+(2018﹣π)0﹣
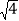 +(
+( )﹣1
)﹣1(2)化简:(a+1)2﹣a(a﹣2)
(3)解方程:x2+4x﹣5=0;
(4)2x2﹣3x﹣1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】“安全教育,警钟长鸣”,为此,某校随机抽取了九年级(一)班的学生对安全知识的了解情况进行了一次调查统计图1和图2是通过数据收集后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:

(1)此次调查共抽查了多少名学生;
(2)补全统计图;
(3)在扇形统计图中,对安全知识的了解情况为“较差”部分所对应的圆心角的度数是多少;
(4)若全校有1800名学生,估计对安全知识的了解情况为“很好”的学生共有多少名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,健民体育活动中心从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据健民体育活动中心消费者的需求量,活动中心决定用不超过2550元钱购进甲、乙两种羽毛球共50筒,那么最多可以购进多少筒甲种羽毛球?
相关试题

