【题目】某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为3.6米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.6米,看台最低点A与旗杆底端D之间的距离为16米(C,A,D在同一条直线上).
(1)求看台最低点A到最高点B的坡面距离;
(2)一面红旗挂在旗杆上,固定红旗的上下两个挂钩G、H之间的距离为1.2米,下端挂钩H与地面的距离为1米,要求用30秒的时间将红旗升到旗杆的顶端,求红旗升起的平均速度(计算结果保留两位小数)(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)
参考答案:
【答案】
(1)
解:在Rt△ABC中,
AB= ![]() =6米
=6米
(2)
解:AC= ![]() =4.8米,
=4.8米,
则CD=4,.8+16=20.8米,
作FP⊥ED于P,
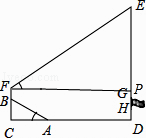
∴FP=CD=20.8,
∴EP=FP×tan∠EFP=13.52,
DP=BF+BC=5.2,
ED=EP+PD=18.72,
EG=ED﹣GH﹣HD=16.52,
则红旗升起的平均速度为:16.52÷30=0.55,
答:红旗升起的平均速度为0.55米/秒
【解析】(1)根据正弦的定义计算即可;(2)作FP⊥ED于P,根据正切的定义求出AC,根据正切的概念求出EP,计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.
(1)依题意补全图1;
(2)猜想AG和DH的数量关系并证明;
(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )
A. 甲 B. 甲与丁 C. 丙 D. 丙与丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-
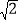 ,0),B(0,2),C(-2,2).
,0),B(0,2),C(-2,2).(1)当直线l的表达式为y=x时,
①在点A,B,C中,直线l的近距点是 ;
②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;
(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“国家卫生城市”复检,某市环卫局准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)每个A型垃圾箱和B型垃圾箱各多少元?
(2)现需要购买A,B两种型号的垃圾箱共300个,分别由甲、乙两人进行安装,要求在12天内完成(两人同时进行安装).已知甲负责A型垃圾箱的安装,每天可以安装15个,乙负责B型垃圾箱的安装,每天可以安装20个,生产厂家表示若购买A型垃圾箱不少于150个时,该型号的产品可以打九折;若购买B型垃圾箱超过150个时,该型号的产品可以打八折,若既能在规定时间内完成任务,费用又最低,应购买A型和B型垃圾箱各多少个?最低费用是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
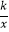 的图象经过点A(﹣1,4),直线y=﹣x+b(b≠0)与双曲线y=
的图象经过点A(﹣1,4),直线y=﹣x+b(b≠0)与双曲线y= 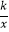 在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.
在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点. 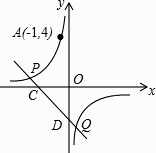
(1)求k的值;
(2)当b=﹣2时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.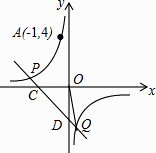
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明想探究函数
 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:x
…
-3
-2
-1
1
2
3
…
y
…
2.83
1.73
0
0
1.73
2.83
…

小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数
 的一条性质:_____________.
的一条性质:_____________.
相关试题

