【题目】 如图,在菱形![]() 中,点
中,点![]() 在对角线
在对角线![]() 上,且
上,且![]() ,
,![]() 是
是![]() 的外接圆.
的外接圆.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 求
求![]() 的半径.
的半径.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
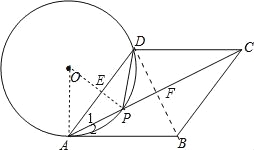
试题分析:(1)连结OP、OA,OP交AD于E,由PA=PD得弧AP=弧DP,根据垂径定理的推理得OP⊥AD,AE=DE,则∠1+∠OPA=90°,而∠OAP=∠OPA,所以∠1+∠OAP=90°,再根据菱形的性质得∠1=∠2,所以∠2+∠OAP=90°,然后根据切线的判定定理得到直线AB与⊙O相切;
(2)连结BD,交AC于点F,根据菱形的性质得DB与AC互相垂直平分,则AF=4,tan∠DAC=![]() ,得到DF=2
,得到DF=2![]() ,根据勾股定理得到AD=
,根据勾股定理得到AD=![]() =2
=2![]() ,求得AE=
,求得AE=![]() ,设⊙O的半径为R,则OE=R﹣
,设⊙O的半径为R,则OE=R﹣![]() ,OA=R,根据勾股定理列方程即可得到结论.
,OA=R,根据勾股定理列方程即可得到结论.
试题解析:(1)连结OP、OA,OP交AD于E,如图,
∵PA=PD,
∴弧AP=弧DP,
∴OP⊥AD,AE=DE,
∴∠1+∠OPA=90°,
∵OP=OA,
∴∠OAP=∠OPA,
∴∠1+∠OAP=90°,
∵四边形ABCD为菱形,
∴∠1=∠2,
∴∠2+∠OAP=90°,
∴OA⊥AB,
∴直线AB与⊙O相切;
(2)连结BD,交AC于点F,如图,
∵四边形ABCD为菱形,
∴DB与AC互相垂直平分,
∵AC=8,tan∠BAC=![]() ,
,
∴AF=4,tan∠DAC=![]() =
=![]() ,
,
∴DF=2![]() ,
,
∴AD=![]() =2
=2![]() ,
,
∴AE=![]() ,
,
在Rt△PAE中,tan∠1=![]() =
=![]() ,
,
∴PE=![]() ,
,
设⊙O的半径为R,则OE=R﹣![]() ,OA=R,
,OA=R,
在Rt△OAE中,∵OA2=OE2+AE2,
∴R2=(R﹣![]() )2+(
)2+(![]() )2,
)2,
∴R=![]() ,
,
即⊙O的半径为![]() .
.
-
科目: 来源: 题型:
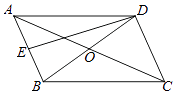
查看答案和解析>>【题目】如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个.
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】 已知,在
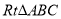 中,
中, 是
是 边上的一个动点,将
边上的一个动点,将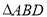 沿
沿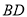 所在直线折叠,使点
所在直线折叠,使点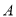 落在点
落在点 处.
处.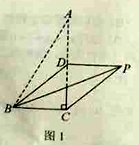
(1)如图1,若点
 是
是 中点,连接
中点,连接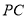 . ①写出
. ①写出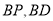 的长;②求证:四边形
的长;②求证:四边形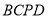 是平行四边形.
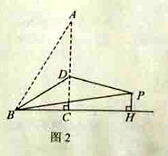
是平行四边形.(2)如图2,若
 ,过点
,过点 作
作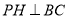 交
交 的延长线于点
的延长线于点 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】将铁丝围成的△ABC铁框平行地面(水平)放置,并在灯泡的垂直照射下,在地面上的影子是△A′B′C′,那么△ABC与△A′B′C′之间是属于( )
A.对称变换B.平移变换C.位似变换D.旋转变换
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不等式变形中正确的是( )
A.若a<b,则a-b<b-1B.若a>b,则ac2>bc2
C.若a-3>-3,则a>0D.若ab>0,则a<0,b<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】由中国发起创立的“亚洲基础设施投资银行”的法定资本金为100 000 000 000美元,用科学记数法表示为美元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
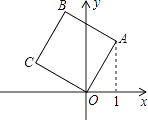
A.(﹣2,1)
B.(﹣1,2)
C.(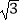 ,﹣1)
,﹣1)
D.(﹣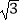 ,1)
,1)
相关试题

