Question

【题目】已知：点D是等腰直角三角形ABC斜边BC所在直线上一点（不与点B重合），连接AD．

（1）如图1，当点D在线段BC上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．求证：BD=CE，BD⊥CE；

（2）如图2，当点D在线段BC延长线上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．请画出图形。上述结论是否仍然成立，并说明理由；

（3）根据图2，请直接写出AD、BD、CD三条线段之间的数量关系。

Answer 1

【答案】(1)、证明过程见解析；(2)、证明过程见解析；(3)、2AD2=BD2+CD2

【解析】

试题分析：(1)、首先根据等腰直角三角形的性质得出∠ABC=∠ACB=45°，然后根据同角的余角相等得出∠BAD=∠CAE，从而说明△BAD和△CAE全等，得出BD=CE，∠ACE=∠ABC=45°，然后根据∠BCE=∠ACB+∠ACE得出垂直；(2)、连接CE，然后根据(1)的同样证法得出答案；(3)、根据∠EAD=90°AE=AD得出ED=AD，然后根据Rt△ECD的勾股定理得出答案.

试题解析：(1)、如图1，∵∠BAC=90°，AB=AC， ∴∠ABC=∠ACB=45°， ∵∠DAE=90°，

∴∠DAE=∠CAE+∠DAC=90°， ∵∠BAC=∠BAD+∠DAC=90°， ∴∠BAD=∠CAE，

在△BAD和△CAE中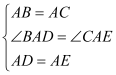， ∴△BAD≌△CAE（SAS）， ∴BD=CE，∠ACE=∠ABC=45°．

∴∠BCE=∠ACB+∠ACE=90°， ∴BD⊥CE；

(2)、如图2，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．

与(1)同理可证CE=BD，CE⊥BD；

(3)、2AD2=BD2+CD2，

∵∠EAD=90°AE=AD， ∴ED=AD， 在RT△ECD中，ED2=CE2+CD2， ∴2AD2=BD2+CD2