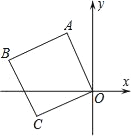
【题目】如图,平面直角坐标系中有一正方形OABC,点C的坐标为(﹣2,﹣1),则点A坐标为_____,点B坐标为_____.
参考答案:
【答案】 (﹣1,2) (﹣3,1)
【解析】分析:过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,根据点C的坐标求出![]() ,再根据正方形的性质可得
,再根据正方形的性质可得![]() ,再求出∠AOD=∠COE=∠BCF,然后求出△AOD≌△COE≌△BCF,根据全等三角形对应边相等可得AD=CE=BF=1,OD=OE=CF=2,然后求解即可.
,再求出∠AOD=∠COE=∠BCF,然后求出△AOD≌△COE≌△BCF,根据全等三角形对应边相等可得AD=CE=BF=1,OD=OE=CF=2,然后求解即可.
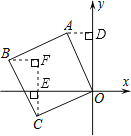
详解:如图,过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,
∵C(2,1),
∴OE=2,CE=1,
∵四边形OABC是正方形,
∴OA=OC=BC,
易求∠AOD=∠COE=∠BCF,
又∵![]()
∴△AOD≌△COE≌△BCF,
∴AD=CE=BF=1,OD=OE=CF=2,
∴点A的坐标为(1,2),EF=21=1,
点B到y轴的距离为1+2=3,
∴点B的坐标为(3,1).
故答案为:(1,2);(3,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
-
科目: 来源: 题型:
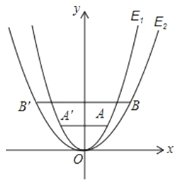
查看答案和解析>>【题目】如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
(1)求m的值;
(2)求抛物线E2所表示的二次函数的表达式;
(3)在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+2与y轴相交于点A0,过点A0作
 轴的平行线交直线y=0.5x+1于点B1,过点 B1作
轴的平行线交直线y=0.5x+1于点B1,过点 B1作 轴的平行线交直线y=x+2于点A1,再过点
轴的平行线交直线y=x+2于点A1,再过点 作
作 轴的平行线交直线y=0.5x+1于点B2,过点 B2作
轴的平行线交直线y=0.5x+1于点B2,过点 B2作 轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1 ,A2 ,A3 ,…,与直线y=0.5x+1上的点B1,B2,B3,…,则A7B8的长为( )
轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1 ,A2 ,A3 ,…,与直线y=0.5x+1上的点B1,B2,B3,…,则A7B8的长为( )
A.64 B.128 C.256 D.512
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A6比图A2多出“树枝”( )

A. 32 B. 56 C. 60 D. 64
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
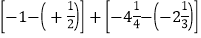 ; (2)-18+5-(-7)-(+11);
; (2)-18+5-(-7)-(+11);(3)
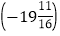 ×240; (4)
×240; (4)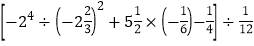 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)3x+2(x2-y)-3(2x2+x-
 y),其中x=
y),其中x= ,y=-3;
,y=-3;(2)3a2c-[2ab2-2(abc-
 ab2)+3a2c]-abc,其中a=-
ab2)+3a2c]-abc,其中a=- ,b=2,c=3.
,b=2,c=3.
相关试题

