搜索
【题目】如图，
、
分别切
于
、
，
，
是劣弧
上的点（不与点、重合），过点的切线分别交、于点
、
．则
的周长为（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】C
【解析】
根据切线长定理由PA、PB分别切⊙O于A、B得到PB=PA=10cm，由于过点C的切线分别交PA、PB于点E、F，再根据切线长定理得到EA=EC，FC=FB，然后三角形周长的定义得到△PEF的周长=PE+EF+PF=PE+EC+FC+PF，用等线段代换后得到三角形PEF的周长等于PA+PB即可得答案.
∵PA、PB分别切⊙O于A、B，
∴PB=PA=10cm，
∵EA与EC为⊙的切线，
∴EA=EC，
同理得到FC=FB，
∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF
=PE+EA+FB+PF
=PA+PB
=10+10
=20（cm）．
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一根弹簧的长度为10厘米，当弹簧受到
千克的拉力时（不超过10），弹簧的长度是
（厘米），测得有关数据如下表所示：拉力
（千克）1
2
3
4
…
弹簧的长度
（厘米）
…
（1）写出弹簧长度
（厘米）关于拉力（千克）的函数解析式；（2）如果拉力是10千克，那么弹簧长度是多少厘米？
（3）当拉力是多少时，弹簧长度是14厘米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明骑自行车去学校，最初以某一速度匀速行驶，中途自行车发生故障，停下来修车耽误了几分钟，为了按时到校，他加快了速度，仍保持匀速行驶，结果准时到校，到校后，小明画了自行车行进路程s(km)与行进时间t(h)的图象，如图所示，请回答：
(1)这个图象反映了哪两个变量之间的关系？
(2)根据图象填表：
时间t/h
0
0.2
0.3
0.4
路程s/km
(3)路程s可以看成时间t的函数吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校科技小组进行野外考察，途中遇到一片湿地，为了安全、迅速通过这片湿地，他们沿着前进路线铺了若干块木块，构筑成一条临时近道，木板对地面的压强
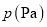是木板面积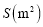
的反比例函数，其图像如下图所示：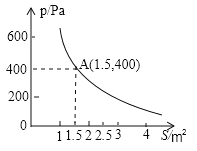
（1）请直接写出这一函数表达式和自变量取值范围；
（2）当木板面积为
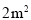时，压强是多少？（3）如果要求压强不超过
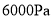，木板的面积至少要多大？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂修建了甲、乙两个水池，最大蓄水量都是1200立方米，如果甲池有水480立方米，乙池蓄满水，甲池每小时进水80立方米，乙池每小时放水100立方米.
（1）分别写出甲、乙两池的水量
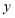与时间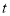
的函数解析式；（2）甲、乙两池同时进水、放水，经过几小时两个水池内的水一样多？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中，真命题的是（ ）
A.两边和一角对应相等，两三角形全等
B.两腰对应相等的两等腰三角形全等
C.两角和一边对应相等，两三角形全等
D.两锐角对应相等的两直角三角形全等
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）问题发现,
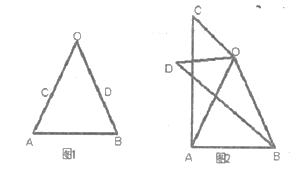
如图1，在
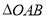中，
，
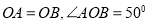是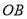
上一点，将点绕点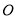
顺时针旋转50°得到点
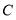，则
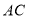与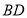
的数量关系是________________________。（2）类比探究
如图2，将（1）中的
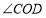绕点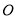在平面内旋转，（1）中的结论是否成立，并就图2的情形说明理由。（3）拓展延伸
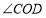绕点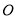在平面旋转，当旋转到
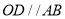时，请直接写出
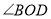度数。
相关试题
