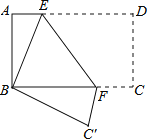
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在![]() 处,折痕为EF,若
处,折痕为EF,若![]() ,
,![]() ,则
,则![]() 和
和![]() 的周长之和为
的周长之和为![]()
![]()
A. 3 B. 4 C. 6 D. 8
参考答案:
【答案】C
【解析】
由折叠特性可得CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,推出∠ABE=∠C′BF,所以△BAE≌△BC′F,根据△ABE和△BC′F的周长=2△ABE的周长求解.
将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,
由折叠特性可得,![]()
∵![]()
∴∠ABE=∠C′BF,
在△BAE和△BC′F中,
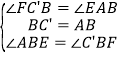 ,
,
∴△BAE≌△BC′F(ASA),
∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3,
△ABE和△BC′F的周长=2△ABE的周长=2×3=6.
故选:C.
-
科目: 来源: 题型:
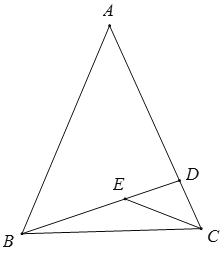
查看答案和解析>>【题目】如图,在△ABC中,BD⊥AC于D.若∠A:∠ABC:∠ACB=3:4:5,E为线段BD上任一点.
(1)试求∠ABD的度数;
(2)求证:∠BEC>∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )

A.
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
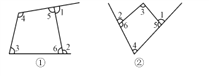
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是
 内任意一点,
内任意一点, ,点M和点N分别是射线OA和射线OB上的动点,
,点M和点N分别是射线OA和射线OB上的动点, 周长的最小值是5cm,则
周长的最小值是5cm,则 的度数是
的度数是


A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l:
 ,过点M(1,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M5的坐标为_____.
,过点M(1,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M5的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=30°,BC=2
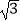 ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( ) 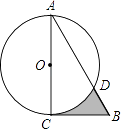
A.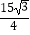 ﹣
﹣ 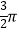
B. ﹣
﹣ 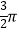
C.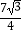 ﹣
﹣ 
D.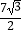 ﹣
﹣ 
相关试题

