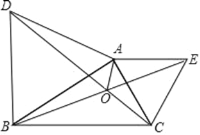
【题目】如图,分别以△ABC 的边 AB,AC 向外作等边三角形 ABD 和等边三角形 ACE,线段 BE 与 CD 相交于点 O,连接 OA.
(1)求证:BE=DC;
(2)求∠BOD 的度数;
(3)求证:OA 平分∠DOE.
(4)猜想线段 OA、OB、OD 的数量关系,并证明.
参考答案:
【答案】(1)见解析;(2) 60°;(3)见解析;(4)见解析.
【解析】
(1)根据等边三角形性质得出AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,求出∠BAE=∠DAC.根据SAS证△ABE≌△ADC即可;(2)根据全等求出∠ADC=∠ABE,在△DOB中根据三角形的内角和定理和∠ADB=∠DBA=60°即可求出答案;
(3)过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.根据三角形的面积公式求出AN=AM,根据角平分线性质求出即可;(4)在 OD 上截取一点 G,使得 OG=OA.由(2)(3)知∠AOD=∠BOD=∠AOE=60°,故可证△AOG 是等边三角形,根据等边三角形性质得到AG=AO,∠GAO=60°,进而得到∠DAG=∠BAO,根据SAS证△DAG≌△BAO,进而可得OD=OG+DG=OA+OB.
(1)证明:∵△ABD 和△ACE 都是等边三角形,
∴ AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,
∴∠BAC+∠CAE=∠BAC+∠BAD, 即∠BAE=∠DAC.
在△ABE 和△ADC 中
∵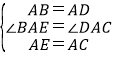 ,
,
∴△ABE≌△ADC(SAS),
∴BE=DC.
(2)解:由(1)知:△ABE≌△ADC,
∴∠ADC=∠ABE
∴∠ADC+∠BDO=∠ABE+∠BDO=∠BDA=60°
∴在△BOD 中,∠BOD=180°﹣∠BDO﹣∠DBA﹣∠ABE
=180°﹣∠DBA﹣(∠ADC+∠BDO)
=180°﹣60°﹣60°
=60°.
(3)证明:过点 A 分别作 AM⊥BE,AN⊥DC,垂足为点 M,N.
∵由(1)知:△ABE≌△ADC,
∴S△ABE=S△ADC
∴![]() BEAM=
BEAM=![]() DCAN
DCAN
∴AM=AN
∴点 A 在∠DOE 的平分线上, 即 OA 平分∠DOE.
(4)解:结论:OD=OA+OB.
理由:在 OD 上截取一点 G,使得 OG=OA.
由(2)(3)可知:∠AOD=∠BOD=∠AOE=60°,
∵OG=OA,
∴△AOG 是等边三角形,
∴AG=AO,∠GAO=60°,
∵∠DAB=∠GAO=60°,
∴∠DAG=∠BAO,
∵AD=AB,AG=AO,
∴△DAG≌△BAO(SAS),
∴DG=BO,
∴OD=OG+DG=OA+OB.
-
科目: 来源: 题型:
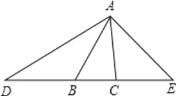
查看答案和解析>>【题目】如图,在△ABC 中,∠ABC=50°,∠ACB=80°,延长 CB 至 D,使 DB=BA,延长 BC 至 E,使 CE=CA,连接 AD 和 AE,求∠D,∠DAE 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展“阳光体育一小时”活动,按学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题:
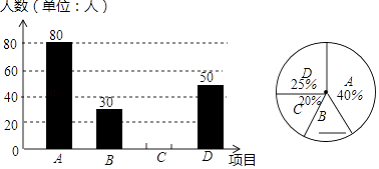
(1)本次共调查了名学生;
(2)在扇形统计图中,“B”所在扇形的圆心角是度;
(3)将条形统计图补充完整;
(4)若该中学有1200名学生,喜欢篮球运动的学生约有名. -
科目: 来源: 题型:
查看答案和解析>>【题目】证明:如果两个三角形中有两条边和其中一边上的中线对应相等,那么这两个三角形全等.(写出已知,求证,画出图形并证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有点a,b,c三点

(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读思考
我们知道,在数轴上|a|表示数a所对应的点到原点的距离,这是绝对值的几何意义,由此我们可进一步地来研究数轴上任意两个点之间的距离,一般地,如果数轴上两点A、B 对立的数用a,b表示,那么这两个点之间的距离AB=|a﹣b|.也可以用两点中右边的点所表示数的减去左边的点所表示的数来计算,例如:数轴上P,Q两点表示的数分别是﹣1和2,那么P,Q两点之间的距离就是 PQ=2﹣(﹣1)=3.
启发应用
如图,点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0
(1)求线段AB的长;
(2)如图,点C在数轴上对应的数为x,且x是方程2x+1=
 x﹣8的解,
x﹣8的解,①求线段BC的长;
②在数轴上是否存在点P使PA+PB=BC?若存在,直接写出点P对应的数:若不存在,说明理由.
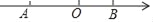
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:直线 a,b,c 表示三条相互交叉而建的公路,现在要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
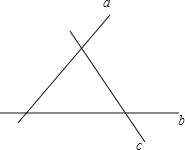
A. 1 个 B. 2 个 C. 3 个 D. 4 个
相关试题

