Question

【题目】在下列括号内填理由：已知：如图，AC∥DE，CD、EF分别为∠ACB、∠DEB的平分线．

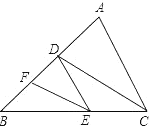
求证：CD∥EF

证明：∵AC∥DE〔已知）

∴ ＝ （ ）

∵CD、EF分别为∠ACB、∠DEB的平分线．（已知）

， （ ）

∴∠DCB＝∠FEB

∴CD∥EF（ ）

Answer 1

【答案】∠ACB；∠BED；两直线平行，同位角相等；∠ACB；∠BED；角平分线的定义；同位角相等，两直线平行

【解析】

根据平行线的性质和判定，以及角平分线的定义就进行证明即可．

证明：∵AC∥DE（已知）

∴∠ACB＝∠BED（ 两直线平行，同位角相等）

∵CD、EF分别为∠ACB、∠DEB的平分线．（已知）

（角平分线的定义）

∴∠DCB＝∠FEB

∴CD∥EF（ 同位角相等，两直线平行），

故答案为：∠ACB；∠BED；两直线平行，同位角相等；∠ACB；∠BED；角平分线的定义；同位角相等，两直线平行．