【题目】在学习了一次函数图像后,张明、李丽和王林三位同学在赵老师的指导下,对一次函数![]() 进行了探究学习,请根据他们的对话解答问题.
进行了探究学习,请根据他们的对话解答问题.
(1)张明:当![]() 时,我能求出直线与
时,我能求出直线与![]() 轴的交点坐标为 ;
轴的交点坐标为 ;
李丽:当![]() 时,我能求出直线与坐标轴围成的三角形的面积为 ;
时,我能求出直线与坐标轴围成的三角形的面积为 ;
(2)王林:根据你们的探究,我发现无论![]() 取何值,直线总是经过一个固定的点,请求出这个定点的坐标.
取何值,直线总是经过一个固定的点,请求出这个定点的坐标.
(3)赵老师:我来考考你们,如果点![]() 的坐标为
的坐标为![]() ,该点到直线
,该点到直线![]() 的距离存在最大值吗?若存在,试求出该最大值;若不存在,请说明理由.
的距离存在最大值吗?若存在,试求出该最大值;若不存在,请说明理由.
参考答案:
【答案】(1) (3,0), ![]() ; (2) (2,1); (3)
; (2) (2,1); (3) ![]() ;
;
【解析】
(1) 张明:将k值代入求出解析式即可得到答案;
李丽: 将k值代入求出解析式,得到直线与x轴和y轴的交点,即可得到答案;
(2) 将![]() 转化为(y-1)=k(x-2)正比例函数,即可求出;
转化为(y-1)=k(x-2)正比例函数,即可求出;
(3) 由图像![]() 必过(2,1)设必过点为A,P到直线的距离为PB,发现直角三角形ABP中PA是最大值,所以当PA与
必过(2,1)设必过点为A,P到直线的距离为PB,发现直角三角形ABP中PA是最大值,所以当PA与![]() 垂直时最大,求出即可.
垂直时最大,求出即可.
解:(1)张明: 将![]() 代入
代入![]()
得到y=-x-2×(-1)+1
y=-x+3
令y=0 得-x+3=0,得x=3
所以直线与![]() 轴的交点坐标为(3,0)
轴的交点坐标为(3,0)
李丽:将![]() 代入
代入![]()
得到 y=2x-3
直线与x轴的交点为(![]() ,0) 直线与y轴的交点为(0,-3)
,0) 直线与y轴的交点为(0,-3)
所以直线与坐标轴围成的三角形的面积=![]()
(2) ∵![]() 转化为(y-1)=k(x-2)正比例函数
转化为(y-1)=k(x-2)正比例函数
∴(y-1)=k(x-2)必过(0,0)
∴此时x=2,y=1
通过图像平移得到![]() 必过(2,1)
必过(2,1)
(3)
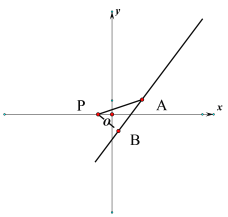
由图像![]() 必过(2,1)
必过(2,1)
设必过点为A,P到直线的距离为PB
由图中可以得到直角三角形ABP中AP大于直角边PB
所以P到![]() 最大距离为PA与直线垂直,即为PA
最大距离为PA与直线垂直,即为PA
∵ P(-1,0)A(2,1)
得到PA=![]()
答:点P到![]() 最大距离的距离存在最大值为
最大距离的距离存在最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个等腰直角三角形
 沿斜边上的高
沿斜边上的高 剪下,与剩下部分能拼成一个平行四边形
剪下,与剩下部分能拼成一个平行四边形 ,如图(1).
,如图(1).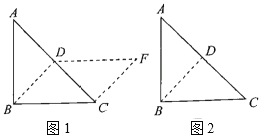
(1)想一想,判断四边形
 是平行四边形的依据是_____________________________________.(用平行四边形的判定方法叙述)
是平行四边形的依据是_____________________________________.(用平行四边形的判定方法叙述)(2)按上述方法做一做,请你拼一个与图(1)位置或形状不同的平行四边形。并在图(2)中面出示意图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
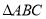 中,
中, ,
,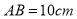 ,
,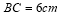 ,若点
,若点 从点
从点 出发以每秒
出发以每秒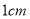 的速度向点
的速度向点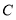 运动,设运动时间为
运动,设运动时间为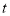 秒
秒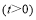 .
.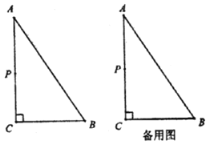
(1)若点
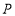 恰好在
恰好在 的角平分线上,求出此时
的角平分线上,求出此时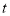 的值;
的值;(2)若点
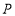 使得
使得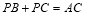 时,求出此时
时,求出此时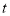 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划销售甲、乙两种产品共
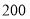 件,每销售
件,每销售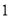 件甲产品可获得利润
件甲产品可获得利润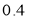 万元, 每销售
万元, 每销售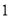 件乙产品可获得利润
件乙产品可获得利润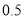 万元,设该商场销售了甲产品
万元,设该商场销售了甲产品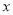 (件),销售甲、乙两种产品获得的总利润为
(件),销售甲、乙两种产品获得的总利润为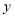 (万元).
(万元).(1)求
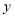 与
与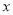 之间的函数表达式;
之间的函数表达式;(2)若每件甲产品成本为
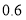 万元,每件乙产品成本为
万元,每件乙产品成本为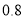 万元,受商场资金影响,该商场能提供的进货资金至多为
万元,受商场资金影响,该商场能提供的进货资金至多为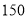 万元,求出该商场销售甲、乙两种产品各为多少件时,能获得最大利润.
万元,求出该商场销售甲、乙两种产品各为多少件时,能获得最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下结论同时成立的是( )
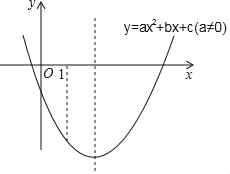
A.
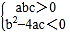 B.
B. 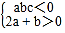 C.
C. 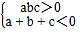 D.
D. 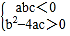
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
 的坐标是
的坐标是 ,动点
,动点 从原点O出发,沿着
从原点O出发,沿着 轴正方向移动,以
轴正方向移动,以 为斜边在第一象限内作等腰直角三角形
为斜边在第一象限内作等腰直角三角形 ,设动点
,设动点 的坐标为
的坐标为 .
.
(1)当
 时,点
时,点 的坐标是 ;当
的坐标是 ;当 时,点
时,点 的坐标是 ;
的坐标是 ;(2)求出点
 的坐标(用含
的坐标(用含 的代数式表示);
的代数式表示);(3)已知点
 的坐标为
的坐标为 ,连接
,连接 、
、 ,过点
,过点 作
作 轴于点
轴于点 ,求当
,求当 为何值时,当
为何值时,当 与
与 全等.
全等. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E、F.求证:OE=OF.

相关试题

