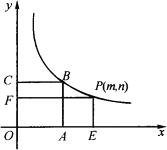
【题目】如图,正方形OABC的面积为9,点O为左边原点,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,点B在函数
轴上,点B在函数![]() 的图象上,点P
的图象上,点P![]() 是函数
是函数![]() 图象上的任意一点,过点P分别作
图象上的任意一点,过点P分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
(1)求B点坐标和![]() 值;
值;
(2)当![]() 时,求P点坐标.
时,求P点坐标.
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)当
;(2)当![]() 时,P点坐标为
时,P点坐标为![]() 或
或![]() .
.
【解析】试题分析:(1)由正方形的面积,利用正方形的面积公式求出正方形的边长,确定出OA及AB的长,得到点B的坐标,将B的坐标代入反比例函数解析式中即可求出k值;
(2)分两种情况考虑:①当点P在点B的左边时,不重合部分为矩形PMCF,将P的坐标代入第一问确定出的反比例函数解析式中,得到mn的值,根据P及B的坐标,表示出PM与CM,利用矩形的面积公式表示出矩形PMCF的面积,将mn的值及已知的面积代入,即可求出m的值,进而得到n的值,确定出此时P的坐标;②当点P在点B的右边时,不重合部分为矩形ANPE,由P及B的坐标表示出AE及PE,利用矩形的面积公式表示出矩形ANPE的面积,将mn的值及已知的面积代入求出n的值,进而求出m的值,确定出此时P的坐标,综上,得到所有满足题意的P的坐标.
试题解析:解:(1)∵正方形OABC的面积为9,∴OA=OC=AB=BC=3,∴B(3,3).又∵点B(3,3)在函数![]() (k>0,x>0)的图象上,∴将B的坐标代入反比例函数解析式得:
(k>0,x>0)的图象上,∴将B的坐标代入反比例函数解析式得: ![]() =3,即k=9;
=3,即k=9;
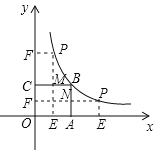
(2)分两种情况:
①当点P在点B的左侧时,矩形OEPF和正方形OABC不重合部分为矩形PFCM.∵P(m,n)在函数![]() 上,∴mn=9.∵PE=n,ME=BA=3,∴PM=PE﹣ME=n﹣3,又CM=OE=m,∴S=CMPM=m(n﹣3)=mn﹣3m=9﹣3m=
上,∴mn=9.∵PE=n,ME=BA=3,∴PM=PE﹣ME=n﹣3,又CM=OE=m,∴S=CMPM=m(n﹣3)=mn﹣3m=9﹣3m=![]() ,解得:m=1.5,可得n=6,∴点P的坐标为(1.5,6);
,解得:m=1.5,可得n=6,∴点P的坐标为(1.5,6);
②当点P在点B的右侧时,矩形OEPF和正方形OABC不重合部分为矩形ANPE.∵P(m,n)在函数![]() 上,∴mn=9.∵OE=PF=m,NF=AO=3,
上,∴mn=9.∵OE=PF=m,NF=AO=3,![]() ,解得n=1.5,可得m=6,∴点P的坐标为(6,1.5).
,解得n=1.5,可得m=6,∴点P的坐标为(6,1.5).
综上所述:P的坐标为(1.5,6)或(6,1.5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )

A.
B.
C.

D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】运用运算律计算:
(1)0.36+(-7.4)+0.3+(-0.6)+0.64;
(2)(-103)+(+1
 )+(-97)+(+100)+(-1
)+(-97)+(+100)+(-1 );
);(3)(-3
 )+(-2.16)+8
)+(-2.16)+8 +3
+3 +(-3.84)+(-0.25)+
+(-3.84)+(-0.25)+ ;
;(4)(-
 )+3
)+3 +|-0.75|+(-5
+|-0.75|+(-5 )+|-2
)+|-2 |.
|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x+b与双曲线y=
 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,反比例函数y=
 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,再解答问题:
-5
 +7
+7 =-5+(-
=-5+(- )+7+
)+7+ =[(-5)+7]+[(-
=[(-5)+7]+[(- )+
)+ ]=2+
]=2+ =2
=2 .
.上述方法叫做拆项法,依照上述方法计算:
(1)7
 +(-7
+(-7 );
);(2)(-2018
 )+(-2017
)+(-2017 )+4036
)+4036 +(-1
+(-1 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成.
(1)写出每天生产夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?
【答案】(1)
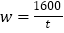 ;(2)
;(2)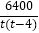
【解析】试题分析:(1)根据实际意义可列出夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)根据题意列出t﹣4对应的式子
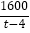 ,与(1)中的式子相减即可.
,与(1)中的式子相减即可.试题解析:(1)由题意可得,函数关系式为:w=
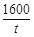 (
( );
);(2)
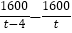 =
=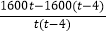 =
=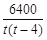 .(或
.(或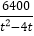 ).
).答:每天多做
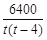 (或
(或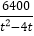 )件夏凉小衫才能完成任务.
)件夏凉小衫才能完成任务.考点:反比例函数的应用.
【题型】解答题
【结束】
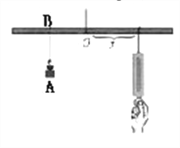
13【题目】如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况。实验数据记录如下:
x(cm)
…
10
15
20
25
30
…
y(N)
…
30
20
15
12
10
…
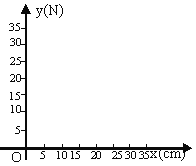
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?
随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
相关试题

