Question

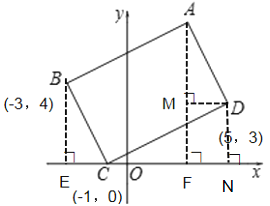
【题目】将□ABCD如图放置，若点B的坐标是(－3，4)，点C的坐标是(－1，0)，点D的坐标是(5，3)，则点A的坐标是______.

Answer 1

【答案】(3，7)

【解析】

过点B作BE⊥x轴于点E，过点A作AF⊥x轴于点于点F，过点D作DM⊥AF于点M，过点D作DN⊥x轴于点N，根据矩形性质可得△BCE≌△ADM，根据矩形判定可得出四边形MDNF是矩形，对边相等，从而求得BE=AM=AF-MF，OF=5-DM，再由点B、C、D坐标即可解答.

解：过点B作BE⊥x轴于点E，过点作A⊥x轴于点于点F，过点D作DM⊥AF于点M，过点D作DN⊥x轴于点N，

∵四边形ABCD是平行四边形，

∴BC∥AD BC=AD，

∵作BE⊥x AF⊥x轴，

∴BE∥ AF ∠BEC=∠AMD=90°，

∴∠EBC=∠MAD，

∴△BEC≌△AMD(AAS)，

∴BE=AM EC=MD ，

∵AF⊥x轴 DM⊥AF DN⊥x轴 B(－3，4) 、C(－1，0)、D(5，3)，

∴四边形DMFN是矩形，EC=OE-OC=3-1=2=DM，

∴OF=ON-FN=ON-DM=ON-DM=5-2=3，AF=AM+MF=BE+DN=4+3=7，

故答案为：（3，7）.