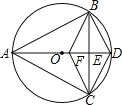
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
参考答案:
【答案】(1)、证明过程见解析;(2)、菱形;理由见解析;(3)、2![]()
【解析】
试题分析:(1)、根据直径得出∠ABD=∠ACD=90°,从而的得出Rt△ABD≌Rt△ACD,然后得出答案;(2)、首先证明△BED≌△CEF,得出CF=BD,即四边形BFCD是平行四边形,根据BD=CD得出菱形;(3)、根据AD是直径,AD⊥BC,BE=CE得出CE2=DEAE,设DE=x,然后求出x的值,根据Rt△CED的勾股定理得出CD的长度.
试题解析:(1)、∵AD是直径, ∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,![]() ∴Rt△ABD≌Rt△ACD, ∴∠BAD=∠CAD,∵AB=AC,∴BE=CE
∴Rt△ABD≌Rt△ACD, ∴∠BAD=∠CAD,∵AB=AC,∴BE=CE
(2)、四边形BFCD是菱形.
∵AD是直径,AB=AC,∴AD⊥BC,BE=CE, ∵CF∥BD,∴∠FCE=∠DBE,
在△BED和△CEF中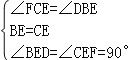 , ∴△BED≌△CEF,∴CF=BD, ∴四边形BFCD是平行四边形,
, ∴△BED≌△CEF,∴CF=BD, ∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,∴BD=CD, ∴四边形BFCD是菱形
(3)、∵AD是直径,AD⊥BC,BE=CE, ∴CE2=DEAE,设DE=x,∵BC=8,AD=10,∴42=x(10﹣x),
解得:x=2或x=8(舍去) 在Rt△CED中,CD=![]() =
=![]() =2
=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李克强总理在2019年的政府工作报告中指出:三大攻坚战开局良好.其中精准脱贫有力推进,农村贫困人口减少1386万,易地扶贫搬迁280万人,数据1386万用科学记数法可表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上A点表示数a,B点表示数b,C点表示数c,且a、c满足|a+3|+(c﹣9)2=0.
(1)a= ,c= ;
(2)如图所示,在(1)的条件下,若点A与点B之间的距离表示为AB=|a﹣b|,点B与点C之间的距离表示为BC=|b﹣c|,点B在点A、C之间,且满足BC=2AB,则b= ;
(3)在(1)(2)的条件下,若点P为数轴上一动点,其对应的数为x,当代数式|x﹣a|+|x﹣b|+|x﹣c|取得最小值时,此时x= ,最小值为 ;
(4)在(1)(2)的条件下,若在点B处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点C处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请表示出甲、乙两小球之间的距离d(用t的代数式表示).
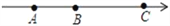
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年5月30日,云南盈江发生6.1级地震.接到灾情报告后,某武警部队迅速组织了两个救援中队赶赴灾区救援.第一中队有x人,第二中队的人数比第一中队的
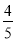 少30人.
少30人.(1)两个中队共有多少人?
(2)由于第一中队任务较重,指挥部决定临时从第二中队调出10人到第一中队,则调动后第一中队的人数比第二中队多多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(n+m)(m﹣n)﹣(4m3n﹣2mn3)÷2mn.
相关试题

