【题目】在平面直角坐标系中,![]() 顶点坐标分别为:
顶点坐标分别为:![]() .线段
.线段![]() 的端点坐标为
的端点坐标为![]() .
.
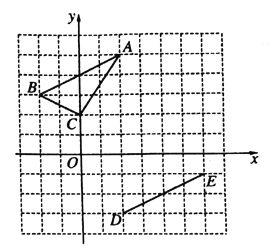
![]() 线段
线段![]() 先向 平移 个单位,再向 平移_ 个单位与线段
先向 平移 个单位,再向 平移_ 个单位与线段![]() 重合;
重合;
![]() 将
将![]() 绕点
绕点![]() 旋转
旋转![]() 后得到的
后得到的![]() 使
使![]() 的对应边为
的对应边为![]() 直接写出点
直接写出点![]() 的坐标;
的坐标;
![]() 写出点
写出点![]() 在旋转过程中所经过的路径
在旋转过程中所经过的路径![]() 的长.
的长.
参考答案:
【答案】(1)![]() 先向右平移
先向右平移![]() 个单位;再向下平移
个单位;再向下平移![]() 个单位与
个单位与![]() 重合;(2)
重合;(2)![]() ;(3)
;(3)![]()
【解析】
(1)直接利用平移的性质得出平移规律即可;
(2)利用旋转的性质得出对应点位置进而得出答案;
(3)根据勾股定理求出PC,利用弧长公式进而求出答案.
解:(1)![]() 先向右平移4个单位,再向下平移6个单位与
先向右平移4个单位,再向下平移6个单位与![]() 重合;
重合;
故答案为:右,4,下,6;
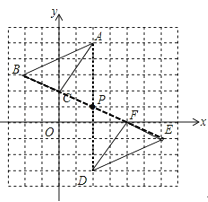
(2)如图所示:将![]() 绕点
绕点![]() 旋转
旋转![]() 后得到的
后得到的![]()
![]() 的对应边为
的对应边为![]()
所以连接AD、BF,两条线段交点即为点P的位置,所以![]() ;
;
(3)由题意得![]() 在旋转过程中所经过的路径
在旋转过程中所经过的路径![]() 的长即为以P为圆心,以PC为半径的半圆长,
的长即为以P为圆心,以PC为半径的半圆长,
根据勾股定理得:CP=![]() ;
;
∴点![]() 在旋转过程中所经过的路径长
在旋转过程中所经过的路径长![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,直线
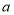 ,
,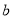 所成的角跑到画板外面去了,你有什么办法作出这两条直线所成角的角平分线?
所成的角跑到画板外面去了,你有什么办法作出这两条直线所成角的角平分线?小明的做法是:
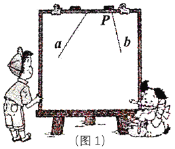
(1)如图2,画
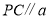 ;
;(2)以
 为圆心,任意长为半径画圆弧,分别交直线
为圆心,任意长为半径画圆弧,分别交直线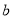 ,
,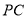 于点
于点 ,
,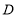 ;
;(3)连结
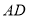 并延长交直线
并延长交直线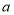 于点
于点 ;
;请你先完成下面的证明,然后完成第(4)步作图:
∵
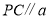
∴
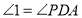 ( )
( )∵以
 为圆心,任意长为半径画圆弧,分别交直线
为圆心,任意长为半径画圆弧,分别交直线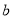 ,
,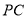 于点
于点 ,
,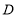
∴

∴
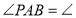
∴
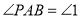
∴以直线
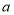 ,
,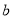 的交点和点
的交点和点 、
、 为顶点所构成的三角形为等腰三角形( )
为顶点所构成的三角形为等腰三角形( )根据上面的推理证明完成第(4)步作图
(4)请在图2画板内作出“直线
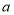 ,
,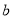 所成的跑到画板外面去的角”的平分线(画板内的部分),尺规作出图形,并保留作图痕迹.
所成的跑到画板外面去的角”的平分线(画板内的部分),尺规作出图形,并保留作图痕迹.第(4)步这么作图的理论依据是: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从
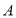 城出发匀速行驶至
城出发匀速行驶至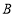 城.在整个行驶过程中,甲、乙两车离
城.在整个行驶过程中,甲、乙两车离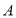 城的距离
城的距离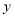 (千米)与甲车行驶的时间
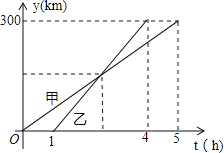
(千米)与甲车行驶的时间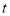 (小时)之间的函数关系如图所示.则下列结论:
(小时)之间的函数关系如图所示.则下列结论:①
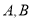 两城相距
两城相距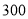 千米;
千米;②乙车比甲车晚出发
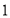 小时,却早到
小时,却早到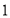 小时;
小时;③乙车出发后
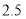 小时追上甲车;
小时追上甲车;④当甲、乙两车相距
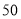 千米时,
千米时,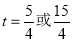
其中正确的结论有( )
A.
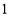 个B.
个B.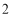 个C.
个C.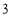 个D.
个D.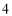 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论的是______________(只填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在开展 “校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单价70元/个.
(1)原计划募捐3400元,购买两种款式的书包共60个,那么这两种款式的书包各买多少个?
(2)在捐款活动中,由于学生捐款的积极性高涨,实际共捐款4800元,如果至少购买两种款式的书包共80个,那么女款书包最多能买多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步普及足球知识,传播足球文化,某市在中小学举行了“足球在身边”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:

(1)获得一等奖的学生有 人;
(2)在本次知识竞赛活动中,A,B,C,D 四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数
 (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
相关试题

