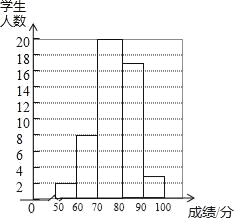
【题目】王老师将本班的“校园安全知识竞赛”成绩(成绩用s表示,满分为100分)分为5组,第1组:50≤x<60,第2组:60≤x<70,…,第5组:90≤x<100.并绘制了如图所示的频率分布表和频数分布直方图(不完整).
(1)请补全频率分布表和频数分布直方图;
(2)王老师从第1组和第5组的学生中,随机抽取两名学生进行谈话,求第1组至少有一名学生被抽到的概率;
(3)设从第1组和第5组中随机抽到的两名学生的成绩分别为m、n,求事件“|m﹣n|≤10”的概率.
分组编号 | 成绩 | 频数 | 频率 |
第1组 | 50≤s<60 | 0.04 | |
第2组 | 60≤s<70 | 8 | 0.16 |
第3组 | 70≤s<80 | 0.4 | |
第4组 | 80≤s<90 | 17 | 0.34 |
第5组 | 90≤s≤100 | 3 | 0.06 |
合计 | 1 |

参考答案:
【答案】(1)补全频数分布直方图见解析;(2)频率分布表中需补(从上到下2,20,50);(2)第1组至少有一名学生被抽到的概率为![]() ;(3)事件“|m﹣n|≤10”的概率为
;(3)事件“|m﹣n|≤10”的概率为![]() .
.
【解析】
(1)根据第2组的频数与频率列式求出学生总人数,然后求出相应的频数与即可,再根据频率之和等于1解答,然后补全统计图;
(2)画出树状图,然后根据概率公式列式计算即可得解;
(3)根据组距,只有被抽到的两人都是同一组方可满足|m-n|≤10,然后根据概率公式列式计算即可得解.
解:(1)学生总人数为:8÷0.16=50,
第1组频数:50×0.04=2,
第3组频数:50×0.4=20,
频数之和为50,频率之和为1;
补全频数分布直方图如图所示,
频率分布表中需补(从上到下2,20,50);
(2)根据题意画出树状图如下:
第1组共2人,将其分别记为a1,a2;第5组共3人,将其分别记为b1,b2,b3;

一共有20种情况,第1组至少有一名学生被抽到的情况有14种,
故第1组至少有一名学生被抽到的概率为P=![]() =
=![]() ;
;
(3)若被抽到的2名学生均来自第1组,其最低分为50,最高分不足60,这样|m﹣n|≤10,符合题意;
若抽到的2名学生均来自第5组,其最低分为90,最高分不超过100,这样|m﹣n|≤10,符合题意;
若抽到的2名学生一名来自第1组,另一名来自第5组,这样30<|m﹣n|≤50,不符合题意,
由此,被抽到的2名学生来自于同一组,
故,事件“|m﹣n|≤10”的概率为P=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某班数学兴趣小组利用数学知识测量建筑物DEFC的高度.他们从点A出发沿着坡度为i=1:2.4的斜坡AB步行26米到达点B处,此时测得建筑物顶端C的仰角α=35°,建筑物底端D的俯角β=30°.若AD为水平的地面,则此建筑物的高度CD约为( )米.(参考数据:
 ≈1.7,tan35°≈0.7)
≈1.7,tan35°≈0.7)
A. 23.1 B. 21.9 C. 27.5 D. 30
-
科目: 来源: 题型:
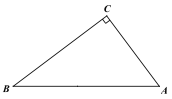
查看答案和解析>>【题目】如图,Rt△ABC,AC⊥CB,AC=15,AB=25,点D为斜边上动点。

(1)如图,过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时,求CE;

(2)如图,在点D的运动过程中,连接CD,若△ACD为等腰三角形,求AD。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示a,点B表示b,且a,b满足

(1)x表示a+b的整数部分,y表示a+b的小数部分,则x= y = ;
(2)若点A与点C之间的距离表示AC,点B与点C之间的距离表示BC,请在数轴上找一点C,使得AC=2BC,求点C在数轴上表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=6,AC=4,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠B=45°,AB=2
 ,AC=4,△DAE是等腰直角三角形,且∠DAE=90°, D在边BC上.
,AC=4,△DAE是等腰直角三角形,且∠DAE=90°, D在边BC上.

(1)求BC的长;
(2)如图1,当点E在AC上时,求点E到BC的距离;
(3)如图2,当点D从点B向点C运动时,求点E到BC的距离的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=
 ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=
 ,AK=
,AK= ,求CN的长.
,求CN的长.
相关试题

