【题目】如图,在△ABC中,AD,AE分别是边BC上的中线和高,
(1)若AE=3cm,S△ABC=12cm2.求DC的长.
(2)若∠B=40°,∠C=50°,求∠DAE的大小.

参考答案:
【答案】(1)CD=4cm;(2)∠DAE=10°.
【解析】
(1)利用三角形的中线平分三角形面积得出S△ADC=6cm2,进而利用三角形面积得出CD的长.
(2)∠B=40°,∠C=50°,根据三角形的内角和得到∠BAC=90°,根据直角三角形斜边的中线等于斜边的一半得到![]() 根据等腰三角形的性质以及三角形外角的性质得到∠ADE=2∠B=80°,即可求出∠DAE的大小.
根据等腰三角形的性质以及三角形外角的性质得到∠ADE=2∠B=80°,即可求出∠DAE的大小.
(1)∵AD,AE分别是边BC上的中线和高,AE=3cm,S△ABC=12cm2,
∴S△ADC=6cm2,
∴![]()
∴![]()
解得:CD=4(cm);
(2)∵∠B=40°,∠C=50°,
∴∠BAC=90°,
又∵AD为中线,
∴![]()
∴∠ADE=2∠B=80°,
又∵AE⊥BC,
∴∠DAE=10°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=
 .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F. 
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(﹣1,0),C(0,3)

(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在P点,使△PCD是以CD为腰的等腰三角形,如果存在,直接写出点P的坐标,如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,
①求直线BC 的解析式;
②当点E运动到什么位置时,四边形CDBF的面积最大?求四边形CDBF的最大面积及此时点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1、∠2之间的数量关系为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(﹣
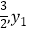 ),(
),(  )是抛物线上两点,则y1<y2其中结论正确的是( )
)是抛物线上两点,则y1<y2其中结论正确的是( ) 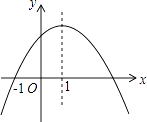
A.①②
B.②③
C.②④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠EAF=180°,求证DE=DF.

相关试题

