【题目】如图,在△ABC中,∠BAC=∠ABC,点P在AB上,如果AD⊥CP,BE⊥CP的延长线,垂足分别为D,E,且BE=CD.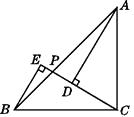
(1)试探求这个图形中还有哪些相等的线段,并给出证明;
(2)试确定△ABC的形状.
参考答案:
【答案】
(1)解:图中相等的线段还有AC=BC,CE=AD.
证明:∵∠BAC=∠ABC,
∴AC=BC.
∵AD⊥CP,BE⊥CP,
∴∠ADC=∠BEC=90°.
又∵BE=CD,
∴Rt△BCE≌Rt△CAD(HL).
∴CE=AD 。
(2)解:△ABC为等腰直角三角形,理由如下 :
∵△BCE≌△CAD,
∴∠EBC=∠ACD.
∵∠EBC+∠BCE=90°,
∴∠ACD+∠BCE=90°,即∠ACB=90°.
又AC=BC ,
∴△ABC为等腰直角三角形 。
【解析】 (1):图中相等的线段还有AC=BC,CE=AD. 根据等角对等边得出AC=BC,根据垂直的定义得出∠ADC=∠BEC=90°,然后利用HL判断出Rt△BCE≌Rt△CAD ,根据全等三角形对应边相等得出CE=AD ;
(2)△ABC为等腰直角三角形,理由如下 :根据全等三角形对应角相等得出∠EBC=∠ACD ,根据直角三角形两锐角互余得出∠EBC+∠BCE=90°,根据等量代换得出∠ACD+∠BCE=90°,即∠ACB=90°,又AC=BC ,从而得出结论△ABC为等腰直角三角形 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解.
根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.
x
…
﹣3
﹣

﹣2
﹣

﹣1
﹣

0

1

2
…
y
…
﹣8
﹣

0

m
﹣

﹣2
﹣

0

12
…
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有 个,分别为 ;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.

-
科目: 来源: 题型:
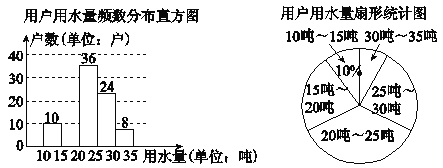
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
-
科目: 来源: 题型:
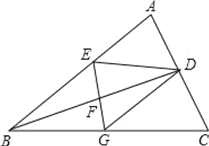
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2,求GC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一个正数的两个平方根分别是2a﹣2和a﹣4,则a的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列现象中是平移的是( )
A.将一张纸对折B.电梯的上下移动
C.摩天轮的运动D.翻开书的封面
-
科目: 来源: 题型:
查看答案和解析>>【题目】用代数式表示“2m与5的差”为( )
A. 2m-5
B. 5-2m
C. 2(m-5)
D. 2(5-m)
相关试题

